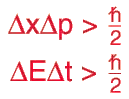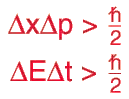Shorter wavelength of photon in detecting a particle

Question

I came across a post on this in the community but wasn't satisfied with the answer,so i am making a new post. Why do we need short wavelength to measure the position of a particle accurately?

The above post has the green marked answer similar to the below description.

I saw in a video that to detect subatomic particles like electrons,we will need shorter wavelengths. And the reason they gave goes along the picture i attached. According to them, if the wavelength of the light is long,the wave the i.e red coloured curvy part won't hit the particle and so we can't see them. But if the wavelength is short,the probability of the curvy part hitting the particle will be more,in short they are saying if $E=hf$ is more then interaction will be more. But i don't understand how it works. What i learnt is

Light is the oscillation of electric and magnetic fields where the thing that oscillates is the fields and not any physical entity. And the light just moves along the straight line in $z$ axis,perpendicular to both the electric and magnetic fields. So,i can't understand how the red curvy part termed as wave is a physical thing. And if that red curvy part is not a physical thing,how can it hit the particle? Please shed some light whether the explanation given in the video is wrong or not,if they are right and my understanding is wrong,kindly enlighten me with the correct concept.

Answer 1

Shorter wavelength of photon in detecting a particle

To start with a single photon does not have a wavelength. It is a quantum mechanical entity, and in mainstream physics described as a point elementary particle of energy $hν$ where $h$ is Planck's constant $ν$ is that frequency a large number of photons of that energy, will have as classical electromagnetic radiation. A photon is not a bundle of classical electromagnetic waves, instead, classical waves develop from the underlying quantum field theory of particles. For quantum entities the wavelength appears in the distribution of many particles , depending on the quantum wavefunction of the particular setup

This can be made clear in the double slit experiment single photon at a time, where the footprint of the photon is seen on the screen, and the accumulation shows the classical interference of light.

. Single-photon camera recording of photons from a double slit illuminated by very weak laser light. Left to right: single frame, superposition of 200, 1’000, and 500’000 frames.

You state

According to them, if the wavelength of the light is long,the wave the i.e red colored curvy part won't hit the particle and so we can't see them. But if the wavelength is short,the probability of the curvy part hitting the particle will be more,in short they are saying if E=hf is more then interaction will be more. But i don't understand how it works.

Translated at the quantum level for individual photon interactions, the probability of a low energy photon ( remember frequency is inversely proportional to wavelength, so a long wavelength means small frequency) to interact with a particle is very small, and will not be measurable, no accumulation as in the plot above. The shorter the wavelength the higher the energy of the photon, and then the plot can happen. The photons interact with the particles building up the walls of the slits.

So you are mixing up in your drawing the quantum ( what you draw as an electron particle is also a quantum mechanical point particle if you look at the table), and the classical electromagnetic radiation. the impinging light is a classical representation and is composed of at least hundred of thousand photons ( as seen the double slit experiment above). If one wants to talk of particles and photons one has to stick to the quantum picture, of photon interacting with electron.

You ask in a comment,

Could you please tell the reason behind,as you said,that low energy photons have a lower chance of interacting?

That is the way the mathematical functions that fit the quantum scattering electron-photon come out, and the theory fits the data very well.

If you know the Heisenberg uncertainty principle, the higher the momentum of two interacting particles the smaller the localization in space. High energy is connected with large momentum, so a high energy photon hitting an electron has a probability of finding it in a smaller volume.

These concepts need the serious study of quantum mechanics.