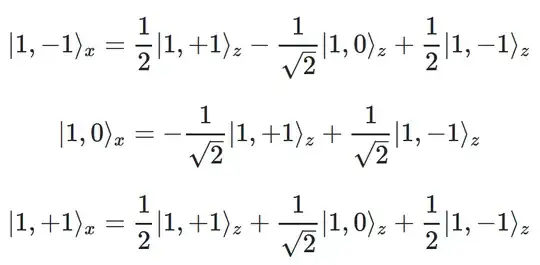Are photon spin and polarization the same thing?

Question

I have posted here regarding this before. I always get conflicting information when I research about this stuff.

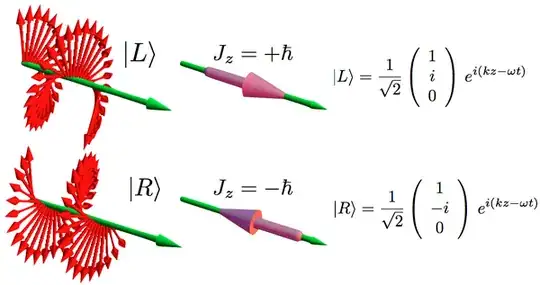
Some people say that a photon spins in or against its direction of motion…meaning if it’s going along the Z axis, from point a to b, it’ll either spin forwards or backwards with respect to its direction of propagation. Others say that it spins circularly(as in left or right with respect to its propagation direction).

Some people also say that polarization of the electric field is the same thing as spin and that the electric field is perpendicular to its direction of propagation.

You can see why I’m confused, especially because I’m finding so much conflicting information. And when it comes to polarizing lenses for a movie theater for example, I’m curious how it works on a quantum level.

I’d really appreciate if someone could tell me in plain English how this works, without using conventional terminology (some people say that left and right handed spin is just conventional and it really spins along its direction of propagation). I also see that angular momentum and orbital momentum are factors in spin as well, which I can’t figure out to be true or not.

Right now I feel like Homer Simpson when he’s clueless(derrr).

The way I learned it originally was that polarization and spin are not the same thing. Polarization is the direction of the electric field in the x and y planes(so horizontal or vertical). But I keep seeing that spin is important with a polarizer(like lenses or an lcd screen pixel). So it almost seems like spin and polarization are the same thing or at least 2 sides of the same coin.

So to sum it up: which direction is a photon actually spinning relative to its direction of propagation along the Z axis? And is polarization really the same as spin? I keep finding conflicting info after hours of googling. So when I think of photons going through a polarizer, some people say they spin left or right due to the electric field, some say that they don’t spin at all..my head hurts!

Any help would be greatly appreciated. My last post on here helped me some, but I was unable to get the info I was looking for in full. Please explain it to me as if I’m a dumb Homer. How does this actually work, in a literal sense(not conventional graph sense)?

Sorry for the long post. I know there are lots of questions. But I just need a basic reply explaining this as a whole. You don’t have to put too much effort into replying. I'm thankful for any help here. So, Thank you!

Edit: if there’s a video that you know of and you think would explain it well, please share it! I’d appreciate it. I’ve found nothing so far. So I’m not being lazy, just not smart enough to fathom it. I feel so stupid haha

Answer 1

It's a really great question. I regularly get confused about this topic and questions around it, and I have to use this topic near every day in my research. Don't be discouraged.

Spin and polarization are not the same. Roger Vadim's answer has the right idea, which I'm just going to expand on and hopefully make clearer.

Polarization is a classical quantity. Notably, what this means is that, for a particular photon, it's defined: you know it, in all relevant axes. For example, if you know the polarization is linear in the $+x$ direction, you know you won't have electric field in the $y$-direction. If the light is circular, you know you have equal field in both directions and you know they're offset by a particular phase ($\pi/2$).

Spin is not like this. Spin is purely quantum. If you know $s_z$ you don't know $s_y$ or $s_x$; in fact you cannot know them.

That said, spin and polarization are intimately connected. As an atomic experimentalist, I have to think about this all the time. We send light to our atoms and expect the electrons to go to certain states. Those transitions have to follow conservation of energy but also conservation of angular momentum. So how do we know where they'll go?

To know it we have to specify a "quantization axis," which is a direction where the angular momentum states of the atom are well-defined. (This corresponds to choosing the "$z$"-axis in the common QM notation.) We typically do this by putting a small magnetic field on the atoms, which splits states of differing angular momentum by small amounts of energy. Then if you "tilt your head" and try to look at the states along a different axis, they'll be ill-defined, in the sense that if you know your atoms to be in, say, $|F=1, m_F=+1\rangle$ ($F$ is some angular momentum) when the magnetic field is in the $+z$ direction, then you won't know the state of your atoms if you suddenly change this magnetic field to a different direction (suddenly so that the electrons' states don't change). This is the same statement that we don't know $s_x$ or $s_y$ if we know $s_z$.

Since we only have knowledge of the electrons' state in this one special direction, whatever light we send in we have to think about its effects relative to that axis. The photons' angular momentum is along its propagation direction, so we have to decompose that direction relative to the quantization axis to figure out the transitions that will happen.

Suppose we send light in along the magnetic field, for example. Then LHC and RHC light induce $\Delta m_F = \pm 1$ or $\sigma^{\pm}$ transitions, so that $s_z = \pm 1$, as you might hope. For linear polarization, we must decompose it into LHC and RHC components, so we get both $\sigma^+$ and $\sigma^-$ transitions.

But what happens if we put in light perpendicular to the magnetic field, say in $+x$? Then linear polarization induces $\pi$ transitions, ones for which $\Delta m_F=0$. And circular polarizations must be decomposed into two linear out-of-phase components, one of which must in turn be both RHC and LHC. So you can actually get $\sigma^+$, $\sigma^-$, and $\pi$ transitions in this case!

These statements correspond to these mathematical ones:

So you see that the spin of the photon, the thing that constraints what transitions you can make, depends on the quantization axis, while the polarization of the light doesn't. So although they're closely connected, they're not the same.

Please ask questions if you have them! I can always get better at understanding this.

Answer 2

Polarization is a classical notion, that is, it can be defined already in classical electrodynamics as a direction of the electric field (or as a manner of this field changing in time, e.g., when talking about circular polarization.)

When electric field is quantized, it can be shown that photons possess angular momentum (spin.) This angular momentum possess the general properties of quantum angular momentum - notably, one can measure simulatenously its magnitude and projection on a selected quantization axis, but not simultaneous projections on different axes. As the quantization axis it is often convenient to chose the direction of the photon propagation, in which case it is an example of helicity, more generally defined in particle physics for all particles.

Thus, when we say that the photon spin projection on the direction of its propagation is $\pm 1$, we are thinking of it as an angular momentum, with obvious classical analogy of a top, rotating clockwise or counterclockwise, which is where it joins with our thinking about circular polarization.

What may add to the confusion is that terms polarization, spin and helicity are often use dinterchangeably.

Answer 3

To answer the question, "What direction is the photon spinning w.r.t. the direction of propagation.", the left hand or right term just describes if its clockwise or anticlockwise (curling your fingers and pointing your thumb out with both your hands illustrates that well, with the thumb being direction and fingers being the rotation).

How it relates to polarisation? Shortest answer is that the "linear" polarisations for an individual photon can be considered as a superposition of the right hand and left hand states, while the circular polarisation states can be considered be combination of the linear states i.e. a superposition of the possible spin states a spin 1 boson (photon) can have, either +1 or -1.

Confusing? Yes, this is short hand so there is plenty of detail missed (here's a great video for more a in-depth look, https://www.youtube.com/watch?v=6sR6RV2znXI), but you can consider it a quirk of quantum superposition. If the photons linear polarisation is measured, its spin becomes uncertain as its current state retains that superposition of |R> and |L>; example |V> = 1/sqrt(2)(|R> + |L>). Then, if its circular polarisation is measured i.e. its spin, its linear polarisation is now uncertain as it sits in that superposition; example |R> = 1/sqrt(2)(|V> +i|H>).

Therefore, I would say that spin is describing the possible angular momentum states a particle can occupy (in this case, +1 for |R>, -1 for |L>), and the polarisation is how those states are orientated in a system.

Answer 4

I am forced to copy the figure from the link I gave you in your duplicate question:

Left and right circular polarization and their associated angular momenta

When a light beam is circularly polarized, each of its photons carries a spin angular momentum (SAM) of $+-h/{2π}$ the ± sign is positive for left and negative for right circular polarizations (this is adopting the convention from the point of view of the receiver most commonly used in optics). This SAM is directed along the beam axis (parallel if positive, antiparallel if negative). The above figure shows the instantaneous structure of the electric field of left (L) and right ( R) circularly polarized light in space. The green arrows indicate the propagation direction.

...

The language of physics is mathematics, and physics cannot be described by words only since the time of Newton, who introduced calculus.

Answer 5

Nobody is actually saying that a photon spins in or against it’s direction of motion. It just sounds like they are saying that, because of the use of conventional terminology.

When we describe a photon there is an arrow that rotates around, like clock-hand of a clock that was thrown flat side first.

When the length of the arrow stays constant, then we have a circularly polarized photon. This photon is non-polarized in such sense that there is no special direction that the arrow has all the time, so orientation of one polarizing lens has no effect on how the photon goes through.

If we have many of these circularly polarized photons, then there appears to be an constant strength electric field that rotates around the same way as the aforementioned arrow does.

If the length of the arrow changes as the arrow rotates, and the length is the longest when the arrow points up and when it points down, then we have a vertically polarized photon.

That vertically polarized photon can pass through a vertical long opening on a screen, because its arrow can fit through nicely, so to speak, although that may be a bad wording.

If we have many of these photons, then there appears to be an non-constant strength electric field that also rotates around like the aforementioned arrow does.

The photon arrow is a "photon absorption probability arrow".

If we have many photons with identical arrows, then a similar arrow as that arrow can be said to describe an electric field's strength and direction.