Contradiction in my understanding of wavefunction in finite potential well

Question

Most things like to occupy regions of lower potential. So the probability amplitude should be higher in a region of lower potential. I denote the potential by V.

However, we also know that the kinetic energy of a particle is given by E-V - the bigger this E-V difference (the lower the V basically), the bigger the kinetic energy, thus the bigger the velocity of that particle. By having a bigger velocity though, this means that less time is spent by the particle in the region, thus a lower wavefunction amplitude.

How do both of these statements reconcile with one another? By looking at the diagram below, we see that we have a decreasing amplitude as we go across to the left. But surely the particle will want to be in a region of lower potential?

Answer 1

Even classically, particles with a fixed total energy spend more time near the turning points since this is where the motion is the slowest. The probably of finding the particle in a small region near the bottom of the well is NOT the largest: it is in fact the smallest.

Thus your statement that the particle wants occupy a region of minimum potential energy refers to another situation, where you want to minimize the total energy of the system. The size of the region, i.e. the distance between the turning points, gets smaller as you decrease the total energy and the turning points get closer to the minimum.

Once it does occupy this region (bounded by the two turning points, for a given total energy), it does not occupy every part of this region with equal probability.

Answer 2

Imagine a perfectly elastic ball dropped vertically onto a flat surface. The ball heads for the point of lowest potential, ie the ground, but because of conservation of energy it bounces back to its initial position and continues to bounce up and down. It spends most of its time near the top of its bounce, because it is ravelling more slowly there, so the probability of finding it at a given instant is highest at the top of the bounce and lowest at the bottom, even though the bottom is the most attractive place to be in terms of PE.

Answer 3

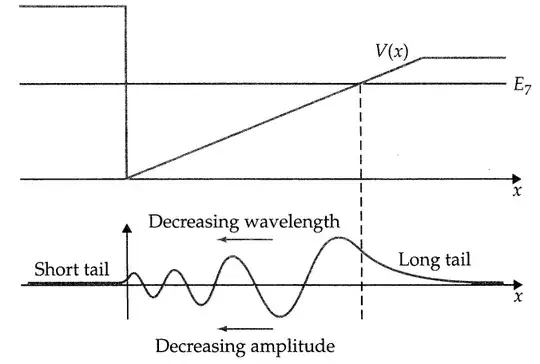
You are probably looking at an energy eigenfunction, a wavefunction which has a definite energy. The statement "$E-V$ is the kinetic energy" does not apply to a single position but to the state as a whole.

This might be a confusing statement so let's compare this to the classical case of a similar well given by $$U(x)=\cases{\infty&$x\leq0$\\\frac{20}{50}x&$0<x\leq 50$\\20& $x<50$}$$ See picture below. I used large values for the width/depth of this well because for the quantum version some effects are shown more clearly.

Imagine you release a particle in this well and you forget about it. What is the probability (density) to find the particle at a position $x$? Well, it is proportional to the time it has spent in the region $[x,x+dx)$ so $$p(x)\propto dt=\frac{dt}{dx}dx=\frac{dx}{v(x)}$$ For a better explanation check out the first link. Like you mentioned, you can easily calculate $v(x)$ using $$v(x)=\sqrt{2(E-U(x))/m}$$. This is shown here:

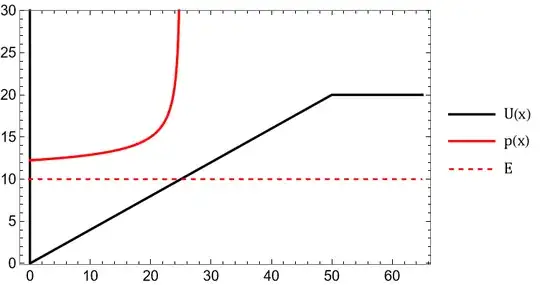
As you can see, the probability density has a sharp peak (vertical asymptote) near the turning point, so it should be of no surprise that the quantum slanted well shows higher probability near the turning point.

Let's now compare this to the quantum well.

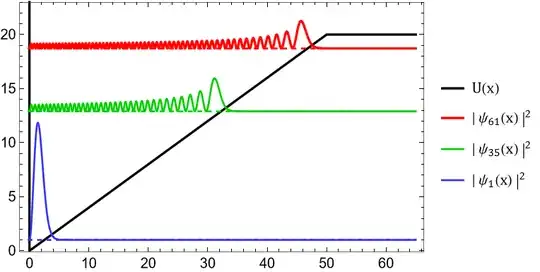
As you can see the wave functions are much better behaved compare to the classical probability function, very nice! Notice that only the ground state "minimizes" the energy. What is shown here are some of the eigenfunction which are all the possible states with definite energy. Since this is just a list there is no reason one of these states should minimize the energy. The energy eigenfunctions are special because they are the only wavefunctions whose probability amplitude is stationary in time.

A state you would find in nature would typically be many of these eigenfunctions added on top of each other, a "superposition" of different eigenfunctions. The probability density of such a state is not stationary and can slosh around in the well.