I read some methods but they're not accurate. They use the Archimedes principle and they assume uniform body density which of course is far from true. Others are silly like this one:
Take a knife then remove your head.
Place it on some scale
Take the reading
re-attach your head.
I'm looking for some ingenious way of doing this accurately without having to lie on your back and put your head on a scale which isn't a good idea.
Here are some methods I came up with:
Newton's Method:
Einstein's Method 1:
Einstein's Method 2:
Heisenberg's Method:
Fermi's Method:
Hooke's Method:
The neck can be modeled as a spring, let's assume its stiffness is $k$.
Mansfield's Method:
Take MRI pictures of the head, which, using my technique will give the 3D density plot of head within few seconds. Now the rest of the problem is just banana cake.
Zeno's Method:
While this method might not be practically efficient, it has incredible philosophical advantages!
Pair Annihilation:
Find your dual(which presumably has opposite quantum numbers than yours), slowly bang your heads together(be careful with the rest of the body). We will measure the released energy(call it $E$), your head's mass will be: $$m=\frac{E}{2c^2} \,.$$
Kitaev's method: Quantum Phase Estimation Algorithm
Upload the quantum state of your head on a quantum computer; this can be done using the quantum teleportation protocol (Be advised, the measurements involved can have some destructive effects on your head!). We define the Mass unitary operator $M$, such that states with known masses are its eigenstates:
$$M|m\rangle = e^{2\pi i \theta_m}|m\rangle\, ,$$ where $\theta_m$ is proportional to the mass of the object the state $|m\rangle$ is representing.
By applying the quantum phase estimation algorithm, with high probability you can get a good estimation of the value $\theta_m$. Better yet would be to have multiple copies of yourself so you can repeat the process and get a more accurate result.
To be completed ...
Petroleum engineers would all provide you with the same answer "use Compton scattering", as this is how the mass density of rock formations gets measured deep in oil wells.
A more complete answer is: Compton scattering can provide you with a measurement of the bulk density of your head. Combine this with a volumetric measurement (dipping your head in a tank and measuring the rise in level), and you're done. You also need a (once off) calibration of the density measurement, as explained below. The big advantage of such a Compton measurement is that it can be repeated and automated at will. Based on accuracies obtained in boreholes, I would expect Compton measurement capable of yielding head weights with a sub-percentage accuracy.
The Compton scattering measurement is done by scanning your head with a gamma ray beam, and measuring the beam attenuation. The gamma ray source should create photons with high enough energies to interact by Compton scattering, but low enough to avoid pair production. 137Cs provides a good source. Although Compton scattering depends on electron density and not on mass density, the measurements can be calibrated to give the correct bulk density for human heads using the ratio of the electron density to the nucleon density. This is based on the observation that the electron density is equal to the bulk density multiplied by Z/A where Z is the average atomic number and A the average atomic weight of the atoms in a human head. In practice, this calibration is best done using heads decapitated from dead bodies.
Steps:
Take a trip to deep space (space suit recommended; means of transportation left as an exercise for the reader). It is important to compute the Hill sphere of your body to make sure it is large enough at this stage. Really it's a Hill-roughly-person-shaped-spheroid-blob, but feel free to assume a spherical you to simplify the calculation.
Deploy a constellation of micro-satellites in orbit around yourself (see Fig. 1).
Carefully track the motion of every satellite.
Process telemetry data to measure the mass distribution of your body, head included.
(optional) Return to Earth.
Profit!
$\hspace{75px}$
$$
\small{
\begin{array}{c}
\textbf{Figure 1:}~\text{Micro-satellites deployed in gravimetric tracking mode.} \\
\text{Careful monitoring of telemetry is required to determine} \\
\text{the mass distribution of the central body.}
\end{array}
}
$$
Thanks a lot for your votes for the "answer" below. Unfortunately I think now the solution does not work. It is great for two slices, but that is the end.
There is another solution that should give 3 slices, which is still a bit short. And I am afraid I do not see how to use the two available steps to start building a recursion :-)
Why ? It is clearly possible to cut the rod in $n$ "homogenous" slices, and then do the $n$ measurements, so as to get a set of $n$ equations with $n$ unknown, the weights of each slice. So we feel the problem conquered. The hitch is that these equations are linearly dependent and have an infinity of solutions, because balancing the rod depends only on the center of mass and the total weight.
Equations are a tricky business, especially when we forget to solve them.
Too bad, especially today, that I am in France right now, and the country has its national holidays: July 14th, aka Bastille day.
So I was hoping that this year, cutting heads could be declared unnecessary.
Let's try to do better for next year.
And do not lose hope... mistakes are interesting too, in their own way, and very educational.
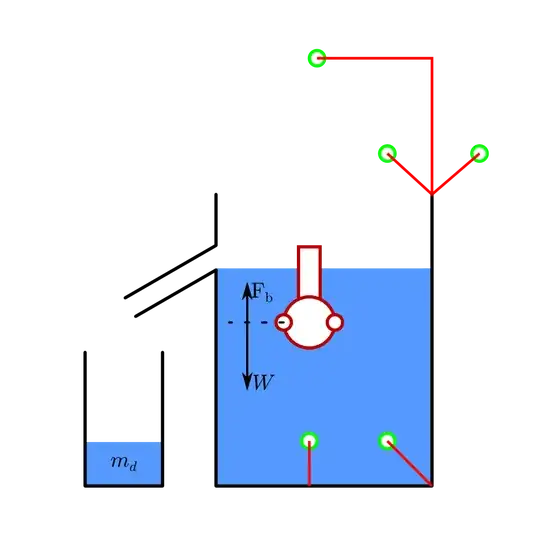
My first reaction was to measure volume with Archimedes's principle. But that does not work since the body density is variable. I was realizing that as @Manishearth made the comment.
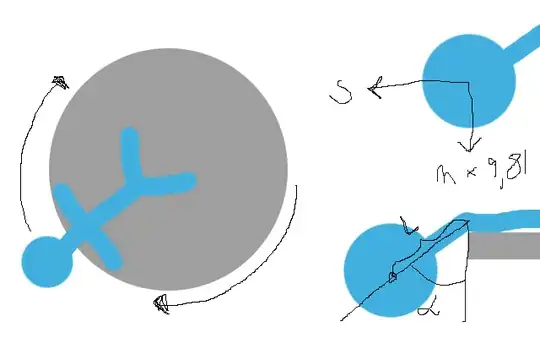
An alternative, is to put yourself on a scale composed of a plank with a central pivot so that only your head is on one side. And you balance the difference between head and body with weights. This does not work a priori because you do not know the mass repartition of your body, and not all the mass has the same distance to the pivot.
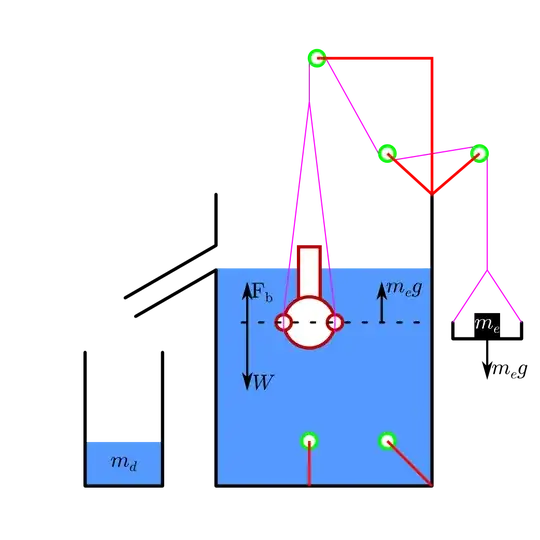
Then what you can do is to do this measurement many times, while moving progressively the body from one side of the plank to the other side, measuring each time the difference in torque due to the weight.
I have not yet worked out the mathematics (and I am not sure I can still do that, probably yes with some effort) but I think that should provide data to determine the longitudinal weight repartition of the body. This reminds me a bit of the way medical scanners work, though this weight problem is probably simpler.
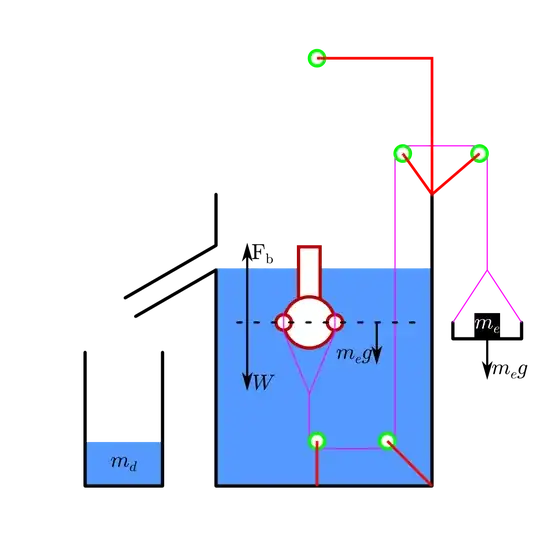
To be convinced that the approach may work, one can first approximate the body as a rod, such that the two halves are each homogeneous but have different weights. Two measurements should allow finding the respective weights of the two halves.
$\hspace{50px}$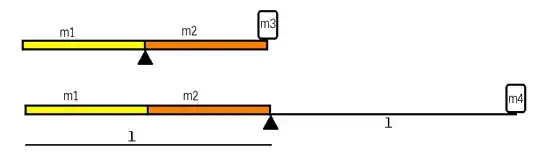
You then get the following equations:
$$ \begin{align} \frac{l}{2}m_1 &~=~ \frac{l}{2} m_2 + lm_3 \\[2.5px] \frac{3l}{4}m_1 + \frac{l}{4}m_2 & ~=~ lm_4 \end{align} $$
The weigths $m_3$ and $m_4$ are known, and the length $l$ is of course measured and known. Thus the equations can be solved to get $m_1$ and $m_2$.
This can be generalized to any number of slices.
In my above quip about being able to do the mathematics is not with respect to resolving a set of linear equations. Rather, I was wondering is there is some kind of transform to express a continuous description of this approach. As I said, I was somewhat inspired by the way medical scanners are working (or maybe the analogy hit me afterwards... hard to know).
This can be generalized to many homogeneous segments approximating the body density repartition.
I would do it like this:
$\hspace{50px}$
!
The muscles of the neck have to be as relaxed as possible so that it approximates a flexible linkage, such that at some point along this linkage (which we can identify as the division between the head and the body, and thus the mass of the head includes a portion of the neck), if we separate the body into two free-body diagrams, there is no net vertical force being exerted between the two.
An assistant can read the scale.
The real difficulty is introduced if you define "head" as that portion of the skeleton, and ajeacent tissue, which excludes all vertebrae of the spine and everything below.
Steps:
Person A lays down on a carousel with its neck over the edge. Person B knocks A out. Person C spins the carousel. B clocks the time. Person D takes pictures of A's head as it goes around.
Measure the angle of the head by looking at the pictures.
Do the vector math.
$\hspace{75px}$
Assume the body to be made of N sections $S_i$ of uniform linear density $\lambda_i$ and length $l_i$ and center of mass $r_i$ (from one end). Increase N as much as you want to get a more accurate reading. The sections need not be of the same length. Try to slice your body into approximately homogeneous sections (homogeneous with respect to mass-per unit length, not volume density).
Now, set up a seesaw-like system with a plank on a log or other pivot. Find a friend or grad student.
Now, sleep on the plank with the boundary between section $S_j$ and section $S_{j+1}$ right above the plank. This will be at a distance $L_j=\sum\limits_{i=1}^{j} l_i$ from one end. Have a friend attempt to balance the system using weights. He will get that some weight $M_j$ will balance the plank when placed at $R_j$.
Repeat this measurement for $j= 1 \to N-1$. Now, write torque equations for each system, assuming that each section has a linear density $\lambda_i$. These equations will be of the form:
$$M_j R_j ~=~ \sum\limits_{i=1}^N \int\limits_{L_j}^{L_j+l_i} \lambda_i x \, \mathrm{d}x \,.$$
Solving the integral, we get:
$$M_j R_j ~=~ \sum\limits_{i=1}^N \frac{\lambda_i}{2} \left(l_i^2 +2l_iL_j \right) \,.$$
You now have $N-1$ equations in the $N$ variables $\lambda_i$. Your $N^\text{th}$ equation will be $\sum l_i\lambda_i =M_{\text{you}}.$
Now, simply calculate the head-mass for the idealized system, and that will be approximately your head mass. Accuracy increases as $N$ does, though you can also increase accuracy by smartly partitioning the system.
The simpler method is decapitation and measurement.
Reattaching the head is, of course, left as an exercise to the reader.
Alternate solution #2:
Break in to LIGO. Go wiggle your head near the interferometer. Memorize the readings on your way out.
(Note: In all seriousness, this probably won't work because LIGO isn't tuned to detect the gravitational waves of head wiggles)
A brilliant book by Tom Cutler: 211 Things a Bright Boy Can Do has a section which shows you how to weigh your head accurately.
This method is easy to understand, and quite practical. It doesn't even involve harming yourself as most of the other methods listed above do. You can actually do it.
Here's the excerpt:
There can’t be many problems more vexing than that of weighing your head. For a start, how do you decide where your head ends and your neck begins? And once you’ve decided this and marked the junction with an indelible pen, what next? It’s a riddle that beat even Archimedes. So here is a method that will produce a good estimate of the weight of your head the next time you find yourself at a loose end.
Required:
· A plastic kiddie pool
· A plastic rainwater barrel
· A plastic bucket
· A plastic measuring jug
· A plastic chair
· Some bathroom scales
· Your head
Method
On a nice day, inflate your kiddie pool in the yard. Divert any bathers from wading into it.
Put your barrel into the pool and fill it (the barrel) with warm water, right up to the top. Do not allow it to overflow.
Shave all your hair off. You’ll get a more accurate measurement this way. Because you are bald no water can be removed by capillary action.
Stand on your chair, hold your breath, and lower your head slowly into the water until it is submerged up to your Adam’s apple. The displaced water will flow down the sides and collect in the bottom of the pool. Slowly take your head out again.
Pour the collected water (from the pool) into your bucket. This is the most annoying part of the experiment because the pool is full of water and you need to move it without spilling any. You can, if you are ambitious, begin the experiment by digging a deep hole in the lawn, into which you now crawl with your bucket, so as to siphon the water from the pool.
Measure, and jot down, the volume of water in your bucket by pouring it into your measuring jug. If the jug’s too small, do it in steps.
Empty the bucket and the jar for the next measurement.
Put the barrel back and fill it to the brim again. Take all your clothes off and weigh yourself. Note down this weight.
Get on the chair and climb carefully into the barrel, completely submerging yourself. After a moment climb out and pour the displaced water into the bucket and then into the measuring jug, keeping a note of the final amount.
Multiply your body weight by the ratio between the two figures. This will give you the weight of your head.
Put your clothes back on.
$\hspace{100px}$
PS: I've added a bit to the text because some parts were unclear. :)
High school chemistry method
Take pictures of your head from at least 129600 different equally spaced out angles. Samples:
$\hspace{100px}$
.
Load them onto the computer, use Mathematica to intersect images at different angles for an approximate 3D model of your face. Find a surface of best fit.
Sample parameterisation: $$ \begin{alignat}{7} x&=0.09 \, \cos\theta \, && \sin\varphi \\ y&=0.09 \, \sin\theta \, && \cos\varphi \\ z&=0.09 \, && \cos\varphi \end{alignat} $$
Use a dropper and a knife to take some small, random samples of your head – the flesh, the cavities (if you're actually following me on this, I'd assume a pretty big one near the top), etc. Your head will become perforated, but that's a small price to pay for the pleasure of finding things out.
$\hspace{250px}$
Measure the densities of these samples – and do it quickly, before they dry up – and plot them as a scalar field across the 3D model.
Now use your perforated brain to calculate a simple volume integral:
$$M=\iiint_V \rho\left(x,y,z\right) ~ \mathrm{d}V$$
Quod erat demonstrandum. Also: mortuus es.
High school physics method
Bang your head on a table. Once it stabilizes, stick a spring balance to it and measure the force required to drag it. Apply $F_k=\mu_kgm$.
$\hspace{100px}$
Just-learnt-quantum-mechanics method
Pluck out your head. Launch it into free space, and keep observing it. Once you have a good data set (this might take a while), apply Schrodinger's equation.
$\hspace{175px}$
The classic way to launch a head into space is via a space shuttle, but there's some probability of a mere human throw achieving escape velocity.
Just-learned-general-relativity method
Same as above, but calculate the metric tensor near your head and compare to the Kerr metric. Here it is, for reference:
$$ c_0^{2} d\tau^{2} = c_0^{2}\left( 1 - \frac{r_{s} r}{\rho^{2}} \right) \mbox{d}t^{2} - \frac{\rho^{2}}{\Delta} \mbox{d}r^{2} - \rho^{2} \mbox{d}\theta^{2} - \left( r^{2} + \alpha^{2} + \frac{r_{s} r \alpha^{2}}{\rho^{2}} \sin^{2} \theta \right) \sin^{2} \theta \mbox{d} \phi^{2} + \frac{2r_{s} r\alpha \sin^{2} \theta }{\rho^{2}} c_0 \mbox{d}t \mbox{d}\phi $$
Just-learnt-special-relativity method
Get into an insulated environment in a power station with 50% efficiency. Bang your head against your antiparticle's to free yourself of fermionic matter. Get someone to use the generated electricity to power a donkey's motion.
$$m=\frac12 (\gamma_{\mathrm{donkey}}-1)m_{\mathrm{donkey}}$$
This method suddenly looks normal
Swap your neck to a spring balance and hang upside down.
$\hspace{225px}$
Here is a way to measure it using the person's moment of inertia. Also, compared to many of the other answers to this question, this method is not only feasible, but actually reasonably safe for the subject.
.Now compute the net moment of inertia: $$I = I_{\text{net}} = I_{\text{gross}} - I_{\text{tare}} \,.$$
For simplicity, I will model the head and body of the subject as if they were thin rectangular plates rotated about the axis at one end.
Let $m_h$ be the mass of the head of the person, and $m_b$ be the mass of their body. We know, then that $m_h + m_b = m$, or in other words, that the masses of their head and body together add up to the mass of the entire person.
$$I = \frac{m_bh_b^2}{3} + \frac{m_bw_b^2}{12} + \frac{m_hl_h^2}{3} + \frac{m_hw_h^2}{12}$$
Solving this equation yields:
$$m_h = \frac{4 l_h^2 m+w_h^2 m+12 I}{4 h_b^2+w_b^2+4 l_h^2+w_h^2}$$
Going further:
If you wished, you could use a more accurate model of the person, resulting in a more complicated equation for their moment of inertia. Also, if one wished to obtain a more accurate measure, one could measure the person's moment of inertia about several different axes, in order to compensate for nonuniformities in the density of the body as a whole, rather than just differences in the density of the head and the rest of the body.
A safe (albeit not entirely comfortable) method is the following:
Ask a partner to hang you upside down using a rope around your ankles. Tell him to swing you with a small amplitude. You relax your body and ask him to measure the swing period. Now bend your head, keep it in fixed position, and again ask your partner to measure your swing period.
Knowing the local gravitational acceleration $g$, and using the expression relating the swing period to the distance the center-of-mass is away from the pivot point: $$t_{\text{swing}}^2 ~=~ \frac{4\pi^2}{g} \, \frac{\int\limits_{0}^{L} m\left(z\right) z \, \mathrm{d}z}{\int\limits_{0}^{L} m \left(z \right) \, \mathrm{d}z}$$ (with $z$ measuring the distance away from the pivot point), from the change in period you can work out the change in the position of your center of mass.
Provided you weigh yourself afterwards (or better yet: yourself including the rope) and provided you have an accurate estimate of the change in height of the center-of-mass of your head (tip: record the scene with a digital video camera, and ensure you have access to reliable information on the center-of-mass of human heads), you get a good estimate of the mass of your head.
You'll need something like this. The green things are pulleys (consider massless, frictionless).
Also, get some ropes, tie them around your feet and gently lower yourself until your head is under the liquid.
$\hspace{100px}$
Measure the mass of the displaced water $m_d$.
At this point, a buoyant force $F_b$ is acting vertically upwards. Weight $W$ is acting downwards.
If weight is more (try and feel with your neck muscles, in which direction the force is acting), make the apparatus as follows.
$\hspace{100px}$
The the strings to your head (the ears or around under your chin is a good spot to tie). Experiment with different weights and obtain a mass $m_e$ such that you feel no force on your neck muscles.
Now $$ \begin{align} W & = m_e g + F_b \\[2.5px] mg & = m_e g + m_d g \end{align} $$
Set the apparatus as follows:
$\hspace{100px}$
.
Obtain a mass $m_e$ in the same way such that you feel no external force.
Now $$ \begin{align} W+m_e g & = F_b \\[2.5px] W &= F_b-m_e g \\[2.5px] W &=m_dg -m_e g \end{align} $$
Now about calculating that force you feel in your neck muscles, you can attach a modified (extremely sensitive)spring balance like instrument which rests between your chin and shoulders, calibrated to indicate "zero" force in space.
One drawback is the slight compressibility of the body(around your neck) which might absorb some of the buoyant force.
The solution has to be static. Any motion through the neck (relative DOF from body) is going to require very detailed modeling of the bones and muscles to achieve the proper result.
I propose a straight up weight of the head, with careful attention in keeping the neck as loose as possible and as horizontal as possible. See below for an example. You want no muscle forces on the neck (apply anesthetic if needed). Now move the head slowly up and down until you get a linear relationship between elevation and head force, and so you need to average the force around where you think the natural position of the neck is.
$\hspace{100px}$
On a turning roundabout, if you pull your body in to the middle, it will speed up due to conservation of angular momentum. If you lean out, it will slow down, for the same reason.
Now, what about if you lie down flat on a large comfy roundabout with your feet at the centre of rotation and your head pointing out. What will happen to the roundabout speed if you are slowly moved inwards until the top your head is at the centre and your feet are out? First it will speed up, and then, after the centre of balance, it will begin to slow down again. The exact way that it does this will tell us a lot about the distribution of mass in your body.
I speculate that, at some expense, it would be possible to build a mechanism that could:
You'd be stuck on it, turning around, for a while. But it has the up-side of not being fatal.
Using computation, and a mathematical process called deconvolution, I believe it would be possible to build up a volumetric mass density map of your whole body. By simply weighing yourself, you can turn densities in to actual masses.
Now, you can decide which part of you is your head, and ask the software to measure its mass.
To get a 3D volume model, the mechanism would have to also roll you over, as well as translating you in $x$ and $y$ (while you gently turn). To obtain a 2D map, which would be sufficient for the head measuring use case, just $x$ and $y$ translation would be sufficient.
I'm not certain this approach works. It may be the case that the measurements are not linearly independent of each other, and that all you will discover is the centre of mass. I have asked another question here on Phy.S.E. about this.
OK, here is my take:
In a large bath immerse the body in salt water so that it floats. Get a photo, the plate perpendicular to the horizontal plane along the body, and measure the height out of water.
Get the volume of body and head by measuring the weight of the body up to the neck and then fully immersed, knowing the density of water.
Suppose for ease of algebra it is two balls:
a large ball with density $\rho_1$, volume $V_1$; and
a small with density $\rho_2$, volume $V_2$ and $\rho_1 < \rho_2$. The mass of $V_2$ + mass of $V_1$ is $M$.
Let the ratio of the height out of water of $V_1$ to the height of $V_2$ be $a$ . We have$$
\rho_1V_1+\rho_2V_2=M
\qquad \text{and} \qquad
\frac{\rho_1}{\rho_2}=a \,,
$$so noting that $\rho_1=a\rho_2$, then$$
a\rho_2V_1+\rho_2V_2=M
\,,$$hence$$\rho_2=\frac{M}{V_2+aV_1}\,.$$
Now with a computer numerical integration one can do an integral over heights in the photo for a real body with irregular features and work with averages.
That gives the mass of head + helmet. Then subtract mass of helmet.
What about MRI? I don't know the specifics, but a single google search reveals this link which suggests one can measure tissue density using it, and it's rather obvious one could also use MRI to reconstruct a 3D image of the head.
Alternatively, measure the relevant tissue densities of a cadaver then use MRI to evaluate the actual volume occupied by each tissue type which could give an estimate.
Let us take the matrix of tensometers as mattress (about 450x150 points 5mm matrix distance). Let us put examine man/woman on this matrix. Then the total weight is sum of partial forces being measured by tensometers multiplied by gravity. Weight of head is the sum of forces measured by tensometers under head multiplied by gravity. To eliminate muscles force of neck, you may apply anesthetic for examined object.
The sophisticated procedure to eliminate forces of neck´s muscles will come soon.
A more accurate solution than the "relax your neck muscles" and similar ones:
Go to the morgue. Cut off the head of a recently deceased person with a similar body type. Measure the ratio of the weights of the head and body. Measure your weight.
Even more accurate: measure the density of the head you just cut off. Now measure the volume of your own head by immersing it into water. The volume of the head does not vary as much as of the body, where muscle, fat, etc. play a role. For better accuracy, cut off many heads for an average.
Archimedes:
Get a bucket big enough to contain your whole body at the most shrinking position (like a baby in the womb).
Take a note for these following weight scale:
Get out of the bucket very slowly so that you don't spill any more water and record the weight as $W_r$. Your Head Weight will be represented as these following formula:
$$ W_h = W_n - (W_t-W_r)$$ Meaning that your head's weight is equal to your naked weight deducted by the weight of overflowed water that flowed out when you enter the bucket.
The most precise result might be provided by the use of a reference head: This solution works if there is at disposal of science the weight and the volume (and possibly additional biometrical data, see below) of any (detached, fresh) head of reference.
Preliminarily, as an introduction, the following solution which works without reference head might not be exact:
You measure your volume and the volume of your head (by water displacement) and your weight, and you derive by pro rata the weight of your head. Problem: Your head may not have the same density as your body.
This problem may be resolved by the use of reference values of a foreign (detached, fresh) head. The pro rata result will be more exact, and it could be affined if additional biometric data are at hand (e.g. the proportion of specific parts of the head and parts of the head which are comparable with the remaining body such as muscles).
Ask someone to Weigh your head while you are asleep(or take some sleeping tablet) with the muscular tension almost zeroed, you can now measure it accurately by just laying on your head on the weighing machine while your whole body is lying flat on the floor at same height as the machine.
Your head weighs 10 pounds.
For some set of circumstances (gravity, posture, sneezing status, hair length) your head will weigh exactly 10 pounds. Any more precise analysis will require more detailed inputs.
If you can find a way to calculate the density of your head by looking at the amount of the head that is - for example - bone, brain or space, and take the density of each of them, then you could get an average density for the whole head. Then simply measure the volume of the head by possibly submerging it and work out the mass.
Of course this isn't accurate in the slightest, but at least it's an answer.
Float free on water. Now lift your head clear of water. Measure displaced water. (Take account of water was displaced by head)
You should be able to do it by jumping off a table onto a spring scale. Simply film the jump with a high speed camera and look for the shockwave that moves through your body as you are landing and note when it reaches your neck. At the same time note the distance the spring has moved (call it point x). Then note how much further the spring moved afterwards to measure your full weight. Now drop a mass off the table that equals moving the spring to point x. Deduct that weight from your weight and you have hour head weight.
ps. you should be able to get rid of the camera and calculate the shockwave/compressionn wave speed using 9.9m per s per s and the height to your neck and height of the table.
You can use the Archimedes principle by not assuming uniform body density. Instead of getting a measure of the density of human's body you can use a corpse body! Usually, the aspect ratio of the brain tissue to other human organs would not change significantly between different persons. So use Archimedes principle on the corpse relevant parts to calculate the difference in the density of the head and the rest of their body then generalize that for your case! Now use a bath hub to calculate the volume of your head and normalize it to your whole body volume. Calculate your head weight and we are done.
You can find them in any medical school
