I have these little pieces of steel:
I can weigh the whole thing on a scale (the one with lines on it is 14.07g), but I just want to weigh part of it (e.g. the green line to the end i.e. excluding the red X).
The weight is not uniformly distributed along the length, so while I could calculate an estimate based on the position of the green line, it wouldn't be sufficiently accurate.
Is there some nondestructive way to weigh just that specific portion of it?
Use a balance to get the mass of the whole steel object. Then, fill a 100 ml graduate cylinder exactly to the 50 ml mark. Place the steel in the graduate cylinder, obtain the new reading, and subtract 50 ml from that reading to obtain the volume of the steel part. From that information, calculate the density of the steel as $\rho = \frac{m}{V}$.
Next, tie a string around the right end of the steel part. Make sure that the graduate cylinder again has exactly 50 ml of water in it. Submerge the steel part up to the green line, obtain the new graduate cylinder reading, and calculate the volume of the steel part that was submerged. Using that volume and the previously calculated density, calculate the mass of the submerged portion.
Here is a method that you could try.
For an object that can be modelled as two pieces of mass $m_1$ and $m_2$, with a COM of each in an unknown position due to a possible variable density, in principle the values could be found like this.
The blue numbers and $F_1$ are known, (numbers made up as an example), but the red numbers are unknown. Below $g$ and $\cos\theta$ terms are omitted as they cancel.
The object is hung from thin cotton or tape at P and the other end rested at a slight angle $\theta$ on the green scale, producing a reading $F_1$
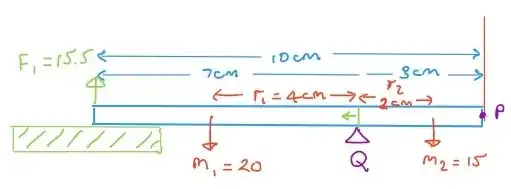
Doing moments (sum of torques = 0) around P, gets our first equation
$$m_1(3+r_1)+m_2(3-r_2)=15.5 \times 10 \tag1$$
swapping the object around and hanging from the other end would give
$$m_1(7-r_1)+m_2(7+r_2)=195 \tag2$$
where the scale $F_2$ would now read 19.5
It's also known that $$m_1+m_2 = 35\tag3$$
However there are 4 red unknowns, another equation is needed.
This time balance the object on a knife edge at $Q$. It would be hard to get an exact balance, so hang a small mass (of value $5$ in this example, not shown) at P, using tape to ensure it's right at the end. The reading on the scale now, by coincidence, is also $F_3 = 5$,
Moments around $Q$ gives a fourth equation
$$5\times 7 + 5 \times 3 + m_2r_2 = m_1r_1\tag4$$
In principle these equations can be solved to recover the unknown red values.
