0

Can two Cartesian inertial frames, in general relative motion, be drawn parallel to each other? A picture in Wikipedia suggests this, but some answers on this site appear to differ.

Consider observers 1 and 2 are in two inertial frames $\Sigma_1$ and $\Sigma_2$ with relative velocity of 2 wrt 1 as $V=(v_x,v_y,v_z)$, $v_x v_y v_z≠0$, sharing origin, $x$-axis, and $xy$-plane at time $0$. Would the $y$-axis of $\Sigma_2$ be perpendicular to $x$-axis of $\Sigma_1$ as reported by observer 1?

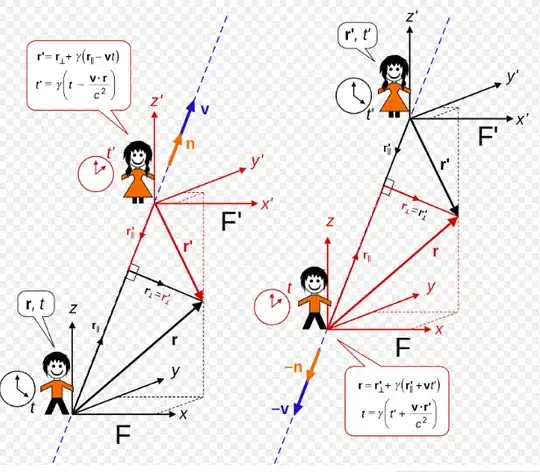
In Wikipedia's picture:

Wikipedia's picture

the coordinates are drawn as if various axes of 1 and 2 form a perfect box, as in Galilean relativity. A comment on the picture's caption

comment below picture

seems to challenge that statement. I tend to think that observer 1's will report the coordinate frames of 2 and 1 won't form a perfect box, various angles won't be 90 degrees. References to texts with a clarification of the issue is appreciated.

Qmechanic
  • 220,844
Maesumi
  • 274
  • 1
  • 2
  • 16

1 Answers1

2

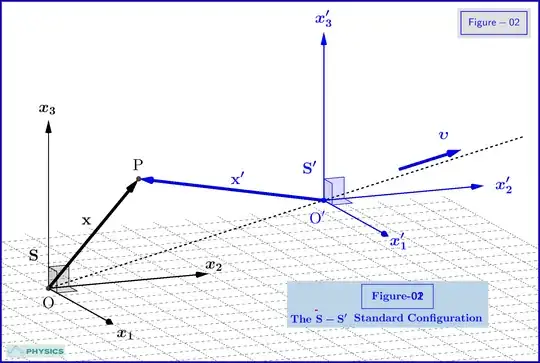
In Special Relativity we couldn't say in general that the axes of two inertial frames $\:\rm S\:$ and $\:\rm S'\:$ in relative translational motion (boost) are parallel, see Figure-02, except of special cases, see Figure-01.

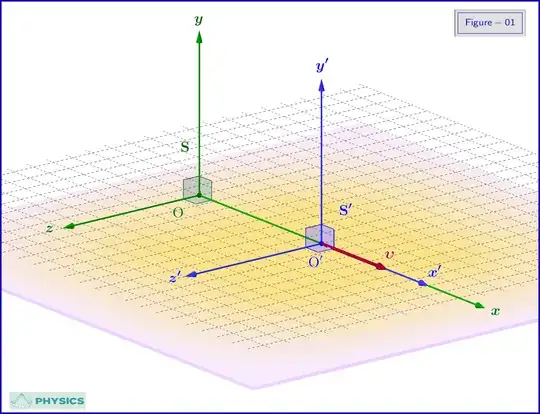
Suppose that a frame $\:\rm S'\:$ is moving uniformly with velocity $\:\boldsymbol\upsilon\:$ with respect to an inertial frame $\:\rm S\:$ and with common $\: x',x-$axes along this velocity as in Figure-01. Planes $\:\mathrm O'x'y'\:$ and $\:\mathrm Oxy\:$ are parallel. We could make the $\: y',y-$axes parallel and the same for the $\:z',z-$axes. This is a special case we could talk about parallel axes between the two inertial frames.

To the contrary, in case of a general boost with velocity $\:\boldsymbol\upsilon$, see Figure-02, we could not talk about parallel axes. For example, the points of the $\:x'_2-$axis in frame $\:\rm S'\:$ at a given moment $\:t'\:$ are simultaneous events in Minkowski space, so the $\:x'_2-$axis is a well-defined straight line in $\:\rm S'$. But these events are not simultaneous in $\:\rm S\:$ so there doesn't exist such a thing or curve or whatever else in $\:\rm S\:$ to be parallel to the $\:x_2-$axis.

enter image description here

enter image description here

ADDENDUM (20-08-2022)

The $\:Ox_1\:$ axis of frame $\:\mathbf S\:$ in Figure-02 is a straight line in frame $\:\mathbf S'\:$ but not parallel to $\:O'x'_1\:$. To derive the details, extract from my answer here Is it a typo in David Tong's derivation of spin-orbit interaction? equations (03) for the Lorentz boost of Figure-02.

Consider that the points of a straight segment (vector) $\:\Delta\mathbf x\:$ are seen simultaneously by observer $\:\mathbf S\:$, that is $\:\Delta t=0\:$, to derive that in $\:\mathbf S'$ \begin{align} \Delta\mathbf{x'} & = \Delta\mathbf{x}\boldsymbol + \dfrac{\gamma^2}{c^2 \left(\gamma\boldsymbol +1\right)}\left(\boldsymbol{\upsilon}\boldsymbol{\cdot} \Delta\mathbf{x}\right)\boldsymbol{\upsilon} \tag{03a}\label{03a}\\ \Delta t' & = \boldsymbol-\,\gamma\dfrac{\boldsymbol{\upsilon}\boldsymbol{\cdot} \Delta\mathbf{x}}{c^2} \tag{03b}\label{03b} \end{align}

Depending on the sign of $\:\Delta t'\:$ return backward or forward in time $\:t'\:$ the points of $\:\Delta\mathbf{x'}\:$ in order to be seen simultaneously by observer $\:\mathbf S'$. The result will be a straight segment (vector) but not parallel to $\:\Delta\mathbf x$.

VoulKons
  • 16,825
  • 2
  • 45
  • 73