One of the derivations of Schroedinger's Equation that I came across assumed the wave function for the particle to be $$\Psi = e^{i(kx-\omega t)} ,$$ and I hardly understand why.
This equation implies that $$\Psi = cos{(kx-\omega t)}+ isin(kx-\omega t). $$
I came across this answer and I believe what it is meant to convey is that the complex expression of the wave function works like a coordinate system that largely simplifies calculations.
I'm trying to understand the physical meaning of this. Does this mean that the wavefunction has a travelling cosine wave along, say, an $x$-axis and a travelling sine wave along the $y$-axis, and the actual wavefunction is a superposition of these?
Sorry if all this sounds absurd. I am an absolute beginner to this course. I'm looking for an intuitive answer more than a mathematical one. I did my research, but it requires some heavy mathematics and I haven't started off with any rigorous math courses at college(I am familiar with basic calculus and linear algebra but not Fourier Transforms or Hilbert Spaces, which often popped up when I looked for explanations.)
- 220,844
- 1,647
2 Answers
The real and imaginary axes have nothing to do with the x, y axes. A wavefunction is a function which asigns a complex number to every point in its domain. Consider a one-dimensional system. The wavefunction asigns to every point $x$ a complex number. You can visualize this a large row of clocks placed on the x-axis. The angle that the clock makes is the phase of the complex number and the length of the hand is the magnitude of the complex number. In your case the magnitude is everywhere 1 so the clocks only rotate.
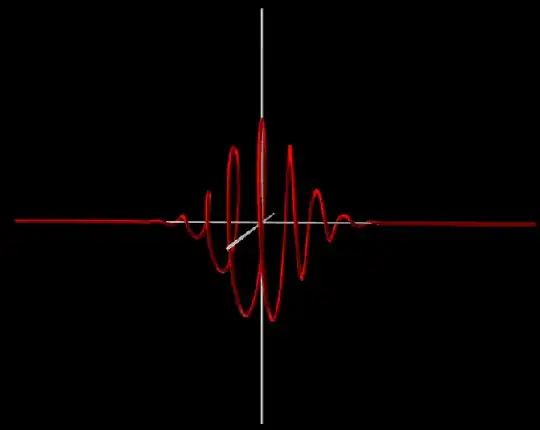
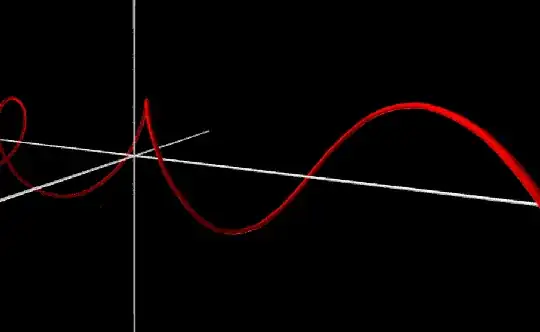
I made a visualization of the 1D Schrödinger equation a long time ago. In the following image the left-to-right axis represents the x-axis. The other two axes show the real and imaginary component of the complex number that is situated at $x$. The distance to the x-axis shows the magnitude of the complex number. Each individual "clock" rotates with a speed that is determined by the Schrödinger equation. In the first animation you can see a wavepacket, a wavefunction that looks like a normal distribution. In the second animation you can see a plane wave which corresponds to your example. In both examples the potential is zero so they are "free particles".
- 19,613
Quantum mechanical waves are complex in nature, unlike electromagnetic or water waves which are modelled by real waves. And this is why we focus on complex waves.
Now, the expression you have pointed out is an example of a complex plane wave. Super-posing some combination of them will give you any wave. Hence we can focus on this as the simplest possible wave.
Its rather like analysing a molecule by focusing on its constituent atoms.
- 14,713