The question is about this video from a youtube channel called Veritasium. It is a popular physics/math youtube channel and topics discussed are usually fact checked and accurate.
The gist of the video (if I got it correctly) is that when we turn on the switch for a bulb in our house, the energy does not flow through the wire due to movement of electrons, but because of electric field travelling directly from the source of the energy to the load.
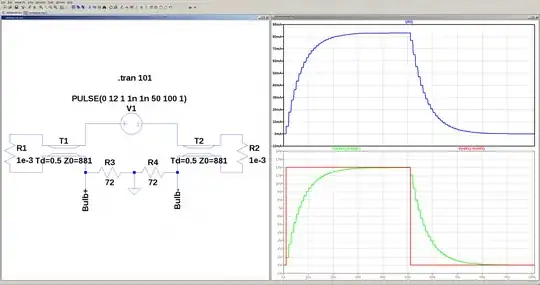
Thus, at the end of the video, he says that when he turns on the switch of the battery/bulb circuit where the battery and bulb are close together but the wires are very long (3*10^9 m, 1 light second), the bulb will light up immediately (in the time it takes for electromagnetic waves to travel from battery to bulb) and not after 1 second as commonly thought. So is he saying this energy flows like a wifi signal from the battery up to the bulb?
I am ok with letting go of my preconceived notions about how electricity actually flows, but I don't know how to visualize what he is saying in the last part of this video. The wire connection from the battery to bulb is clearly important, any other bulb placed nearby but not connected to the wire system will not light up using the same electromagnetic waves that light up the bulb connected to the battery.
If I did manage to connect wires that are 1 light second long, the bulb probably wouldn't light up in practice because of the resistance of the wire. So how can I better understand what this last part of this video is trying to say? I am looking for alternative (but still layman) method of visualizing the concept being explained in this video.
Also, what if the battery and bulb were connected by 1 light second long wire, but were placed 1 light second apart at the two opposite ends of the wire, instead of close together like shown in this video? Would it have taken 1 second for the bulb to light up then? What if the bulb/battery were n*1 light second apart? Would it take n seconds to light up?