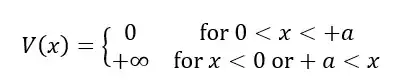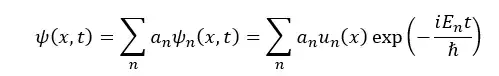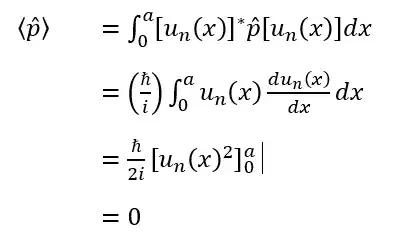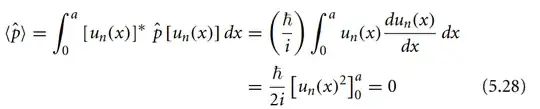For a particle in an infinite well potential given by:
I am able to successful derive the normalized wavefunction as:
$$u_n(x) =\sqrt{2/a}\sin(\frac{n\pi x}{a})$$
where this normalization has the appropriate dimensionality for a one-dimensional wavefunction, but that the sign (or more generally the phase) of the normalization constant is purely conventional, and $-\sqrt{2/a}$ or $\exp(iθ) \sqrt{2/a}$ would serve just as well.
The most general solutions will be linear combination of these energy eigenstates with their associated time-dependence:
The expectation value of momentum in an infinite well stationary state is given by:
•Since the eigenfunctions vanish at the boundaries.
•Thus, the average value of the momentum vanishes in each eigenstate
In the book i am reading for it says this:
The energy eigenstates in this (or any) bound state system can be chosen to be purely real functions (or real with multiplicative complex phases that are independent of position). As the calculation in above illustrates, this implies that the expectation value $⟨p ̂ > ⟩$, which we know must be real, can be written as a purely real integral time i.
I don't understand this
'can be written as a purely real integral time i.'
The extract from the textbook:
Equation