Quantum Tunneling and Negative Kinetic energy

Question

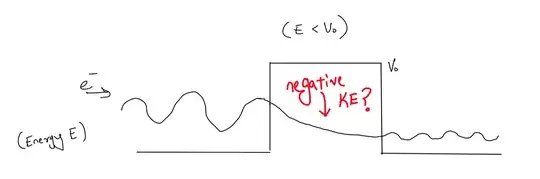
I don't understand how a particle can exist with negative kinetic energy. Consider this scenario:

Here, an electron is tunneling through a potential barrier (The total energy of the electron is less than the potential barrier).

So the math works out pretty well and we find that the wave function has a finite value on the left of the barrier, inside the barrier and also to the right of the barrier.

I'm unable to grasp what is actually happening inside the barrier though:
Like if I make a measurement and the particle turns out to be inside the barrier (it can since the wave function is finite over there), then will we find it there with negative kinetic energy (since potential is greater than total energy)?

Could you explain what actually happens? Do we find it with negative KE and if so, then what does this even imply physically?

Or does the particle get extra energy from somewhere and we find it with non-negative KE and if so, where does it get the energy from?

Answer 1

The kinetic energy in QM is defined as $T=p^2/2m$ and its expectation value $\langle T \rangle = \langle p^2 \rangle /2m$ is always non-negative (this can be proved in general for squares of Hermitian operators).

What happens in the tunneling region then?

Firstly, I don't think it makes much sense to define the kinetic energy of a "slice" of the wavefunction. We could write it like this:

$$\int_a^b \psi^* \frac{\hat p^2}{2m}\psi \, dx$$

with the tunneling region ($E<V_0$) being the interval from $a$ to $b$. In your case, we have $\hat H=\hat T+V_0$, so the integral is just

$$(E-V_0)\int_a^b |\psi|^2 \, dx < 0$$

which does indeed contribute negatively to the average kinetic energy. But remember -- this quantity is not observable and it does not make much sense to talk about it in my opinion.

Secondly, the wavefunction you show above is a time-independent scattering wavefunction. However, you probably consider the process of the particle approaching from the left and being either reflected or tunneling through to the right.

This is more intuitively described by the time-dependent wavepacket picture, where a Gaussian wavepacket approaches from the left and at the end, there are two wavepackets -- one reflected and one transmitted through. This allows one to plot a "movie" of the wavepacket going through -- a great book for this is Tannor's Introduction to QM: A time-dependent perspective, which does this kind of thing in much more detail and rigor.

Answer 2

Kinectic energy corresponds to $p^2/2m$. Inside the barrier, the wavefunction decays exponentially $\psi\propto e^{-\kappa x}$. If we try to extract some momentum information from this form we get, in a hand-waving manner, $e^{i k x} = e^{- \kappa x} \implies k = i \kappa$. That is, the wavenumber is imaginary inside the barrier region. With $p= \hbar k$, we find the momentum is also purely imaginary and $E_{\text{kin}} = (i \hbar \kappa)^2/2m = -\hbar^2 \kappa^2/2m <0$. So indeed, the kinectic energy is negative inside the energy barrier: it must be, since the energy must be the same in all regions for the wavefunction to be an eigenstate.

As a final remark, note that a solution with negative kinectic energy is only possible with appropriate boundary conditions. In particular, we have here regions on both sides where the wavefunction can become of the free-wave form. This type of solution cannot appear with Drichlet boundary conditions of the infinite potential well, for example.