In QFT the propagator is divergent for the on-shell momentum of the particles. When e.g. calculating the amplitude for a box loop, the propagator diverges for on-shell particles running in the box-loop.
Is there a physical interpretation for this divergent behavior?
Yes, there is and you can see it directly in the Källen-Lehmann spectral representation. I won't give you the derivation because it's quite lengthy but when you take this representation for the propagator you can divide the contribution from the one particle states from the contribution from the many particle state in the following manner (for a scalar field, but the results stays the same for spinors and vectors)
$$G(q^2) = \frac{Zi}{q^2-m^2+i\epsilon}+\int_{M_{\text{th}}^2}^\infty\mathrm{d}\mu^2\frac{i\rho(\mu^2)}{q^2-\mu^2+i\epsilon}$$
when you look at the analytic structure of the propagator as a function of $q^2\in\mathbb{C}$ you clearly see a pole given by the physical mass and a cut related to the multiparticle states. In the image there're also highlighted the possible poles due to bound states.
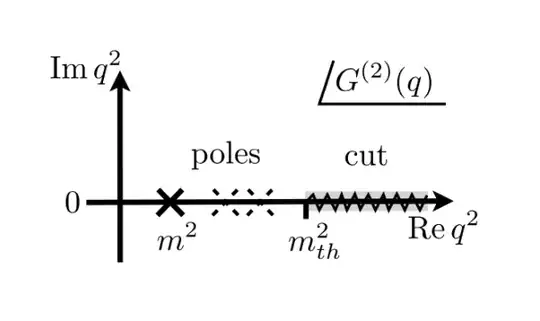
This is quite an interesting result since gives you a correspondence between the physical mass and the unique pole in the propagator. All the multiparticle states do not give singular contributions to the propagator. And most importantly, this result does not rely on perturbation theory. It is go general that it was used bu Weinberg, Goldstone and Salam to give a non-perturbative proof to Goldstone theorem.
I might be wrong about the physical interpretation, but I always thought of it this way: the propagator in configuration space $G(x-y)$ can be interpreted as the probability amplitude for a particle to be created at point $x$, propagate and anihilate at $y$. Then if you think a la Feynman, the path a particle can take between two points is any path in configuration space. In my opinion this necessarly includes paths in which the momentum of the particle does not necessarly need to be on-shell. Then when I think about the representation of $G(x-y)$ in momentum space it becomes obvious for me that we are doing a summation over the momentum's of all this paths, including all this off-shell momentum's. Then I interpret the terms in the summation as follows: the more close the momentum is to be on-shell, the bigger will be its contribution to the integral value. Then what the integral is telling me is that the paths that are more/less probable (the terms that will contribute more to the value of the integral) are those in which the momentum is close/far to be on-shell. Whoa!
