Intuition behind Bernoulli's equation

Question

If water is flowing from a larger subsection $A_1$ of a pipe into a smaller subsection $A_2$ (say, the radius halves), then Bernoulli's principle says that the pressure $P_{A_1} > P_{A_2}$, and $v_{A_1} < v_{A_2}$.

I understand why the velocity would be greater, but why is the pressure at $A_2$ less than at $A_1$? Thinking about it without considering Bernoulli's equation, I'd imagine that the pressure at $A_2$ should be greater due to the smaller area, but this isn't the case. Why not? Physically, what's happening so that the pressure decreases?

Answer 1

Usually, Bernoulli's principle is derived from the conservation law of energy by realising that pressure $P$ is not only a force per area, $F/A$, but also an energy per volume, $\frac{E}{V}=\frac{F\cdot s}{A\cdot s}$. Although this derivative is perfectly fine, I agree that it does not build any intuition. Therefore, I'd like to take a different approach:

The following image sketches your situation

As you said, the increase of the velocity is "natural", if we consider the conservation of mass: In order to obtain the same throughput at position 1 and 2, we need to have $v_1 < v_2$. However, this implies that the fluid accelerates.

What is necessary for the fluid to accelerate? The answer is that the particles, which constitute the fluid, must experience a force difference. Once you grasp this picture and image the individual particles inside the fluids, the pressure difference follows:

• In order to squeeze the particles through the tiny hole, we have to apply some pressure.
• However, once the particles are "inside the hole" (at position 2) the flow is "effortless".

Hence, $P_1 > P_2$.

Answer 2

The fluid has to speed up as it enters the narrower region. That means that the bit of fluid just entering the region has to be being pushed from behind. So the pressure behind it must be larger than in front.

Answer 3

To keep a constant flux of fluid the speed need to increase. Speeding up requires a more kinetic energy per unit volume. That energy needs to come from somewhere, and it comes out of pressure. The fluid accelerates due to the greater pressure on the wide end pushing it along, doing work on the fluid.

Another way of imagining it is to consider a static fluid under pressure that is suddenly released. (Example: a dam with a outlet at the bottom.) The fluid goes from high pressure and 0 speed to low pressure and non-zero speed.

Answer 4

Hydrodynamic equilibrium would help to understand many things. Once you get to it - many fluid laws can be resolved, including Bernoulli's principle and Archimedes buoyant force. If there comes fluid acceleration due to ANY cause - it results in pressure difference too. This can be generalized in general fluid hydrodynamic equilibrium law : $$ -\nabla P + \rho\, \frac {dv}{dt} = 0$$

Consider this schematics :

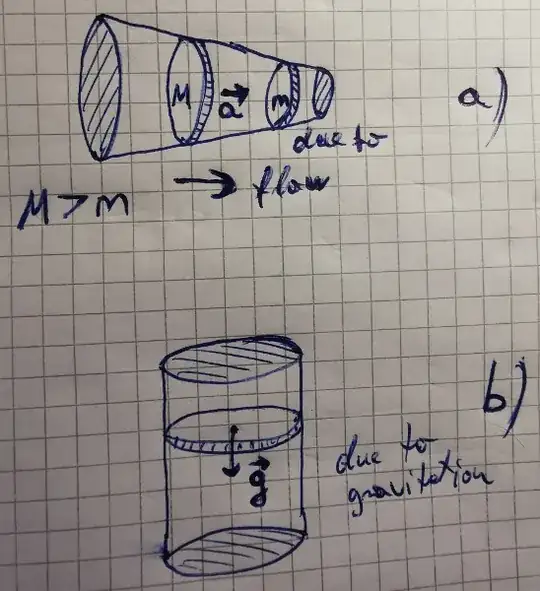
In case (a) fluid acceleration results because unit mass $M$ behind is greater than unit mass $m$ being pushed by it. In case (b) acceleration of unit fluid mass is simply due to Earth gravity.

In both cases acceleration of unit mass produces a pressure gradient, so (a) and (b) are technically equivalent situations.

EDIT

As a bonus for your development of physical intuition. It's interesting to note that movement of people crowd in room under extreme conditions,- such as fire in room,- can be modeled as pseudo-fluid. If people without order tries to rush to nearest exit(s) fast and then pushes each other in the process blindly, then this crowd action results in a great pressure upon those poor people who are in between doors, or near to it. Because only couple of humans can fit through the doors, but behind them are many people wanting the same (so $M > m$ principle). This results in movement acceleration and,- pity,- injuries in some of them. That's why we need strict order leaving such areas - to dismiss crowd pseudo-flow behavior. HTH !

Answer 5

I understood this when I realized that pressure is the cause and velocity is the effect. It simply happens that particles at the wider section outnumber those at the narrow one, which have less room and hence are fewer. (Don’t forget that we talk about an ideal liquid which is, among other things, incompressible.) Thus the outer more numerous particles exert more force per area (pressure) than the inner ones, which are consequently accelerated (their velocity increases).