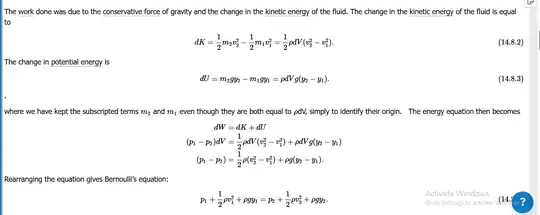Why can't internal forces do work in proof of Bernoulli equation?

Question

So i was reading the proof of Bernoulli equation specifically this one

My doubt is why we didnt include the net work done on the fluid due to the internal forces in the fluid.

So far i got the explaination that for that to happen there needs to be viscous forces or the fluid needs to be compressble. However i dont actually see any proof of why thats the only possibility.

I can see why in a rigid body internal forces cant do any net work but here fluid is not a rigid body.

So how do u actually prove this.

EDIT: I think people misunderstood what i meant by "However i dont actually see any proof of why thats the only possibility" i didnt mean to include the case of compresseble fluids i meant staying in the case of an ideal incompressable fluid how do i prove the internal forces will not do any work on the fluid.

Answer 1

Internal forces don't do work when they are contact forces. Let $\mathcal R$ be some region of the fluid. If the region deforms, then work will be done on the region because each point on the surface of $\mathcal R$ moves some distance under an applied force. But the fluid in this region will perform work on its surroundings that exactly cancels this work. This is a consequence of Newton's third law. Suppose that a small section of $\mathcal R$'s surface displaces by $\delta \boldsymbol \xi$ under a traction (i.e. force per unit area) $\mathbf t$. Then the fluid in $\mathcal R$ applies a traction of $-\mathbf t$ on its surroundings at that point. Since the surrounding fluid also displaces by $\delta \boldsymbol \xi$, the total work is $\delta W = \mathbf t \cdot \delta \boldsymbol \xi + (-\mathbf t) \cdot \delta \boldsymbol \xi = 0$. Note that this result only holds for contact forces.

---

I'll add that the textbook's "proof" of Bernoulli's equation is flawed. It considers the net work on a extended section of the fluid. This might give you the change in kinetic energy of the entire fluid, but Bernoulli's is a statement about the work done on a fluid element as it travels along a streamline. The textbook cobbles together formulas to get the correct result, but it is conceptually flawed.

Answer 2

In physics we usually start with a simple model, which captures the dominant effect. Only if we absolutely need to include details to explain an effect, we modify the simple model to account for these "complications" (second-order effects). Internal forces, e.g. van-der-Waals interactions, and the viscosity of the fluid are complicated modifications. By omitting these details we are able to understand the concept -- the dominant effects.

During your study of physics you will learn to love these simplifications. E.g. nothing is truly a harmonic oscillator, nevertheless, in all subjects of physics you will find some phenomena, which are modelled using this concept.

My advice is to build some intuition of Bernoulli's equation. Details are just in the way of achieving this goal.

Answer 3

The Bernoulli equation is an idealization, i.e. it is, as all of physics is, an approximate model of what it is trying to describe.

To derive the Bernoulli equation you start from the Euler equation and you impose 2 conditions: potential flow (irrotational flow) and incompressibility.

Under those 2 conditions you are unable to model any changes in the internal energy of the fluid, i.e. forces doing work on the fluid to change its internal energy.

If you want to drop the condition of incompressibility (e.g. in gas dynamics), from the Euler equation and the first law of thermodynamics you get the compressible flow Bernoulli equation:

$$h + \frac{v^2}{2}= C$$

where $h$ is enthalpy.

Answer 4

Why can't internal forces do work in proof of Bernoulli equation?

As already pointed out, the net work done by internal forces between fluid parcels is zero. The only internal forces not accounted for in Bernoulli's equation are viscous forces.

But work done by viscous forces involve fluid friction, which dissipates energy as heat. In order to have conservation of mechanical energy (which is the basis of Bernoulli's equation), Bernoulli's equation assumes no viscous forces (i.e., the fluid is assumed inviscid).

Hope this helps.