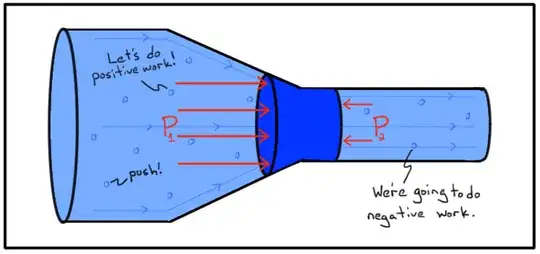
I'm reading Khan Academy which says in this picture:
That P1 > P2 since P1's positive work is greater than P2's negative work. However, I thought forces do work, not pressures. Since F = P * A, I only understand why P1 * A1 > P2 * A2. You can even see in the picture that A1 is greater than A2. How come we can confidently say P1 > P2 then?
First of all look at the conservation of mass in this example, equation of continuity, $A_1\rho_1v_1 = A_2\rho_2v_2 $ assume that the density of the fluid $\rho$ stays constant.
$A_1>A_2 \Rightarrow V_2>v_1$, thus the kinetic energy of the fluid increases when the area decreases.
How is the increase in kinetic energy achieved?
Net work per second must be done on the fluid by the forces, $P_1A_1$ and $P_2A_2$, exerted on the fluid, ie $P_1\color{red}{A_1v_1} - P_2\color{red}{A_2v_2}\Rightarrow P_1>P_2$
We can easily see why:
$$P_1+\frac{1}{2}\rho v_1^2=P_2+\frac{1}{2}\rho v_2^2$$
Also,$$A_1v_1=A_2v_2$$
Plugging in value of $v_2$
$$P_1=P_2+\frac{1}{2}\rho\left(\frac{A_1^2}{A_2^2}-1\right)v_1^2$$
Since $A_1>A_2$, second term is positive. So easily we can deduce that $P_1>P_2$
