How does high velocity cause low pressure?

Question

Bernoulli's principle states that air molecules moving with high velocity create an area of low pressure which in turn causes an object to fly, but how does high velocity cause low pressure?

Answer 1

It is more usual to think that low pressure causes high velocity because a pressure differential implies a force which accelerates the particles of a fluid into the region of low pressure.

OTOH if we know that there is a high velocity, then this must have been caused by a pressure differential, so the logical implication works both ways.

Answer 2

That is a wonderful question. See if there is low pressure in some region then in surrounding areas there will be a high pressure. Imagine a pipe which is constricted in the middle. The high pressure in surrounding areas will cause the molecules to flow into the constricted area with a larger horizontal velocity and less vertical velocity. Essentially the pressure comes due to vertical velocity, when the molecules bounce off the surface below, a lower vertical velocity implies a lower pressure.

Answer 3

Assume air to be incompressible ($M<0.33$) and non viscous flowing under steady condition then according to Bernoulli's principle the sum of pressure energy, kinetic energy and potential energy remain constant. Thus when velocity increases, the pressure decreases at that section to keep the total energy (head) constant.

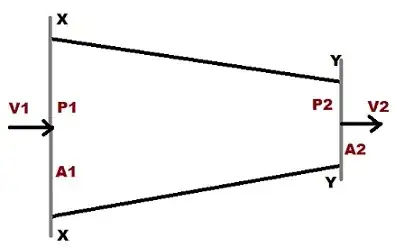
Consider a steady flow of an incompressible and non-viscous fluid with constant density $\rho$ through a horizontal pipe with converging from $A_1$ at section X-X to $A_2$ at section Y-Y (As shown in figure).

From continuity equation $$A_1V_1=A_2V_2\implies V_2=\frac{A_1}{A_2}V_1$$ $$V_2>V_1\quad (\because \ \ A_1>A_2)$$

From Bernoulli's equation: $$\frac{P_1}{\rho g}+\frac{V_1^2}{2g}+Z_1=\frac{P_2}{\rho g}+\frac{V_2^2}{2g}+Z_2$$ $$P_2=P_1-\frac{\rho}{2}(V_2^2-V_1^2)\quad (\because \ \ Z_1=Z_2)$$ $$P_2<P_1\quad (\because \ \ V_2>V_1)$$