Will a falling rod stay in contact with the frictionless floor?

Question

Question

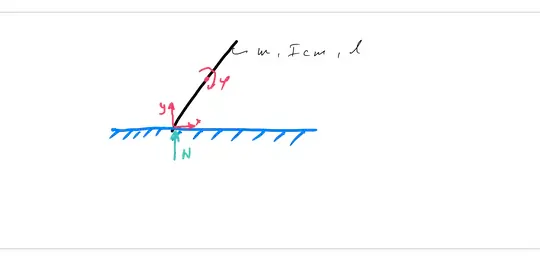
A uniform rod of mass $M$ is placed almost vertically on a frictionless floor. Since it is not perfectly vertical, it will begin to fall down when released from rest.

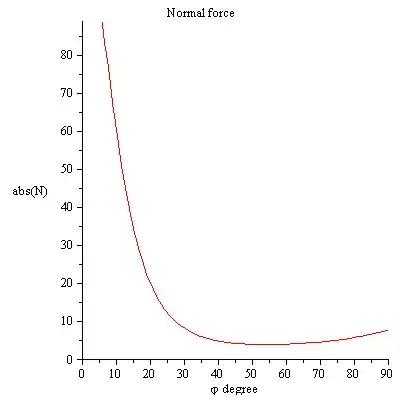
I have seen solutions online for this problem and while solving this problem, it is assumed that the end point of the rod that is in contact with the floor will continue to stay in contact with the floor till the rod, in its entirety, hits the floor horizontally. It is this assumption that lets us determine the normal force from the floor. However, how does one show that this assumption is true? Or is it taken to be an additional constraint of the problem?

Check the figure in D1 to verify if you've got the right setup in mind.

Duplicates in SE:

I believe the OP in D1 has asked the same question (along with other questions) but it has been closed as off-topic. Simon Robinson, one of the answerers in D2, has also expressed concerns about this. I ask this question because it hasn't been addressed properly on SE. I don't feel that the answer to this question is specific only to this vertical rod problem. Instead, I feel that this question is onto something basic that I don't yet understand regarding the necessary constraints that need to be specified in a physics problem.

My Attempt

The problem with this question is that I feel like I have given all the information that's necessary to predict the entire dynamics of the rod's motion after its release. I'm unable to accept the idea that "rod-cannot-lose-contact" constraint must be specified as an additional piece of information to solve this problem. If we accept that it's not an additional constraint, then we should be able to show that the rod's end point cannot lose contact. But, that's the problem. I've been thinking about it for days and I can't seem to find a way to show that.

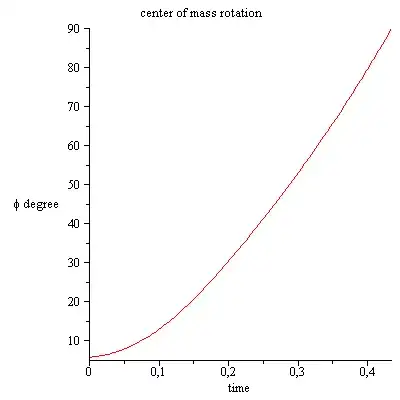
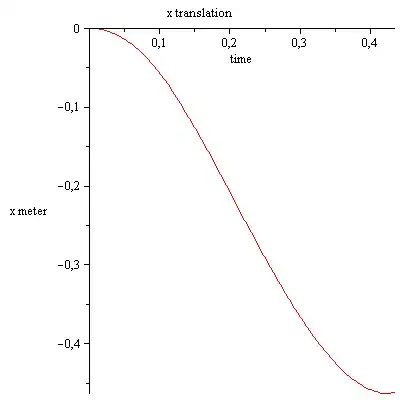
I'm unable to see anything "violated" if it loses contact at some point during its fall. After it loses contact, it simply rotates about the center of mass with constant angular velocity [See $(1)$] and the rod's COM falls down with acceleration $\mathbf{g}$. $$\frac{d\mathbf{L}_{CM}}{dt} = \boldsymbol{\tau}_{CM} \Rightarrow \text{$L_{CM}=I_{CM}\omega\;$ is constant} \tag{1}$$

Thanks for taking the time to read this question. I apologize if I have violated any code of conduct.

Any insight that addresses my question would be greatly appreciated.

Further Clarification, If Needed

Clarifications which will hopefully help PhySE users to better understand my question are made here. Reading the following information is not necessary to answer my question.

It is important to note that even if the rod's bottom end point loses contact with the floor at some point during the fall, the centre of mass of the rod will continue to fall vertically straight down just as before (but now with acceleration $\mathbf{g}$). So, the fact that the COM falls vertically straight down cannot be used to prove that the rod's bottom end point doesn't lose contact with the floor.

COM falls vertically straight down $\not\Rightarrow$ the rod's bottom end point doesn't lose contact with the floor

Michael Seifert · Accepted Answer · 2019-11-26T17:03:47.407

The technique to use in problems like this is to assume that the rod remains in contact with the table, and to then try to figure out whether the normal force ever switches sign for some angle $\theta$ as the rod falls. If it does, then the rod's lower tip will have to leave the table, as a "frictionless table" cannot pull the rod downward; it can only push it upwards. Similar techniques are used in the solution to the classic "puck slides down a frictionless hemisphere" problem, as well as the "toppling ruler" problem.

Actually doing this is something of a mess, but here's a rough sketch. Let $L$ be the length of the rod and $m$ be its mass. Let $I = \frac{1}{4} \beta m L^2$ be the rod's moment of inertia about its center of mass; note that $\beta = \frac{1}{3}$ for a rod of uniform density, while $\beta = 1$ if the mass is concentrated at the tips. This is done to provide a bit more generality; I will assume, however, that the mass distribution is symmetric, so that the center of mass is at the geometric center of the rod.

The ingredients you'll need are:

Geometric constraints: The vertical position of the center of mass of the rod will be $z = \frac{1}{2} L \cos \theta$ (taking positive $z$ to be upwards.) Differentiating this twice, we obtain for the velocity and acceleration of the center of mass $$ v = - \frac{L}{2} \omega \sin \theta, \\ a = - \frac{L}{2} ( \alpha \sin \theta + \omega^2 \cos \theta), $$ where $\alpha$ is the angular acceleration of the rod.
Conservation of energy: Since the table does no work on the tip of the rod, the mechanical energy of the rod is conserved. This gives a relationship between $v$ and $\omega$.
Newton's Second Law (translational): Using Newton's second law, you can relate $a$ and $N$.
Newton's Second Law (rotational): Calculating the torque about the center of mass of the rod, you can find a relationship between $N$ and $\alpha$.

This gives us a system of five equations and five unknowns $\{N, v, a, \omega, \alpha \}$ which can be solved. After going through it, I find that the normal force as a function of $\theta$ is $$ N = \frac{mg \beta (\beta + (1- \cos \theta)^2)}{(\beta + \sin^2 \theta)^2} $$ which is manifestly positive for any value of $\theta$. Thus, the tip of the rod does not leave the table; the table continually maintains an upward normal force as it falls.

score 3 · Answer 2 · edited Nov 27 '19 at 15:27

to see what happens you have to write the equation of motions and then simulate the equations.

we have two generalized coordinate $x$ is the translation on the floor and the rotation of the rod.

starting with the position vector to the center of mass you get:

$$\vec{R}=\left[ \begin {array}{c} l\sin \left( \varphi \right) +x \\ l\cos \left( \varphi \right) \end {array} \right] \tag 1$$

from equation (1) you can obtain the kinetic energy $\quad T=\frac{m}{2}\vec{\dot{R}}^T\,\vec{\dot{R}}+\frac{I_{cm}}{2}\dot{\varphi}^2$ and the potential energy $U=m\,g\,\vec{R}_y$

$\Rightarrow$

The equations of motion:

$${\frac {d^{2}}{d{\tau}^{2}}}\varphi \left( \tau \right) +{\frac {m{l} ^{2}\cos \left( \varphi \left( \tau \right) \right) \sin \left( \varphi \left( \tau \right) \right) \left( {\frac {d}{d\tau}} \varphi \left( \tau \right) \right) ^{2}}{m{l}^{2}+{\it Icm}-m{l}^{2 } \left( \cos \left( \varphi \left( \tau \right) \right) \right) ^{ 2}}}-{\frac {mgl\sin \left( \varphi \left( \tau \right) \right) }{m{ l}^{2}+{\it Icm}-m{l}^{2} \left( \cos \left( \varphi \left( \tau \right) \right) \right) ^{2}}} =0\tag 3$$

$${\frac {d^{2}}{d{\tau}^{2}}}x \left( \tau \right) +{\frac {m{l}^{2} \cos \left( \varphi \left( \tau \right) \right) \sin \left( \varphi \left( \tau \right) \right) g}{m{l}^{2}+{\it Icm}-m{l}^{2} \left( \cos \left( \varphi \left( \tau \right) \right) \right) ^{2}}}-{ \frac { \left( {\frac {d}{d\tau}}\varphi \left( \tau \right) \right) ^{2}l\sin \left( \varphi \left( \tau \right) \right) \left( m{l}^{2}+{\it Icm} \right) }{m{l}^{2}+{\it Icm}-m{l}^{2} \left( \cos \left( \varphi \left( \tau \right) \right) \right) ^{2 }}} =0\tag 4$$

we also have to obtain the normal force (contact force rod floor). To calculate the normal force $N$ I add additional degree of freedom to the direction of the normal force which is $y$ so the position vector is now:

$$\vec{R}= \left[ \begin {array}{c} l\sin \left( \varphi \right) +x \\ l\cos \left( \varphi \right) +y\end {array} \right] $$

the "new" equations of motion are $\ddot{\varphi}=\ldots\,,\ddot{x}=\ldots$ and $\ddot{y}=\ldots$ but we also have the holonomic constraint equation (Lagrange multiplier) .

$y=0\quad \Rightarrow\quad \dot{y}=0\,,\ddot{y}=0$

thus we have enough equations to calculate the contact force $N$

$$N={\frac {{\it Icm}\,ml\cos \left( \varphi \left( \tau \right) \right) \left( {\frac {d}{d\tau}}\varphi \left( \tau \right) \right) ^{2}}{m{l}^{2}+{\it Icm}-m{l}^{2} \left( \cos \left( \varphi \left( \tau \right) \right) \right) ^{2}}}-{\frac {m{\it Icm}\,g}{m {l}^{2}+{\it Icm}-m{l}^{2} \left( \cos \left( \varphi \left( \tau \right) \right) \right) ^{2}}} \tag 5$$

Simulation

I start the simulation with the initial conditions :

$x(0)=0,D(x)(0)=0,\varphi(0)=0.1,D(\varphi)(0)=0.3$

I stop the simulation if the rotation of the rod reach 90 degrees .

you see that the contact force $N$ is greater then zero so the rod has a contact to the floor, you can avoid this situation only if you applied external torque on the rod .

Compare the Normal force with Michael Seifert normal force

with:

$\varphi(0)=0$ and $Icm=\frac{1}{4}\,\beta\,m\,(2\,l)^2$

$$N={\frac {mg\beta\, \left( \beta+ \left( 1-\cos \left( \varphi \right) \right) ^{2} \right) }{ \left( \beta+ \left( \sin \left( \varphi \right) \right) ^{2} \right) ^{2}}} \tag 6 $$

red plot normal force equation (5), blue plot is the normal force equation (6) we get the same results!!!

score 1 · Answer 3 · edited Jun 04 '20 at 16:03

@MichaelSeifert has a very nice answer.

I just want to describe it from a different angle here.

A Calculation

If you only want to investigate if contact is lost at some angle $\theta$, then in this problem it can also be done in the following way: Only the lower end of the rod is in contact with the ground. So for the rod to remain leave contact with the ground after rotating an angle $\theta$, the (upwards) vertical acceleration of the point of contact (POC) due to all forces except the normal force should become non-negative at the very least. One can then imagine that the rod is no longer "falling into the floor" through the POC in this case (it's actually ready to fly away), and so the ground will not act with a non-zero normal force on the rod to slow it down; if it does, because of the geometry of the problem it will only enhance the vertically upward acceleration of POC, which is inconsistent with the constraint.

Now note that acceleration of the POC in the vertical direction at this point due to all forces except the normal force would simply be $\frac{\Omega^2 L}{2} \cos \theta - g $.

$\Bigg[$ We also know $\Omega^2$ in terms of $\theta$ from energy conservation principle (as long as the constraint is obeyed). A quick way to write down the kinetic energy is to note that the rotating rod is instantaneously rotating about an axis perpendicular to the plane of the rod, that passes through the intersection of the vertical through POC and the horizontal line through COM. This would give a kinetic energy of $\frac{1}{2}mL^2\Big[\frac{1}{12}+\frac{\sin^2\theta}{4} \Big] \Omega^2$, which is obtained after a fall of COM by height $\frac{L}{2}(1-\cos\theta)$. $\Bigg]$

If you now really calculate the quantity $\frac{\Omega^2 L}{2} \cos \theta - g $, you will find it to be like the numerator of the expression for $N$ found by @MichaelSeifert, except that it would have a negative sign $-$ this means it can never be positive and so contact can never be lost.

Intuition

We now understand what is responsible for loss of contact $-$ it's the angular velocity of the rod! The larger its magnitude, the greater is the chance of losing contact from the floor. But what happens if you give the rod some initial angular velocity at the start $-$ will contact be lost now? Two cases arise:

Either contact will be lost at the top itself.
Or the contact will never be lost.

You should course work this out mathematically. But there is an intuitive way to understand $-$ assume contact is lost at some point at an angle $\theta \neq 0$ (at least for a small amount of time), then the point of contact has zero velocity in the vertical direction at this moment. From here on, the rod continues to rotate further for an infinitesimal moment without any change in $\Omega$, but then $\frac{\Omega^2 L}{2} \cos \theta - g $ (which was hitherto non-positive) will again become negative because $\theta$ is going to increase a moment later. As soon as that happens, the rod will be falling into the ground through the POC, and the ground will not take kindly to it & exert a normal force in response. And that's a contradiction!

However, if you rotate the rod too fast at the start itself, it's going to lose contact because $\frac{\Omega^2 L}{2} \cos \theta - g $ will be $>0$ at the start itself, and won't become negative an instant later.

This is actually what gives rise to the intuition that the rod will not lose contact for the problem originally posed by you $-$ viz., that since in the original case contact is not lost at the start, it is in fact never lost (as long as the other end of the rod doesn't hit the ground)!

Warning: Do not use this idea in any general problem, because in general the point of contact may not be the same point (for example a rolling disc on a flat plane). So, the general way of course is to implement the constraint and make sure that $N\geq0$ for the constraint assumption to be self-consistent in such problems.