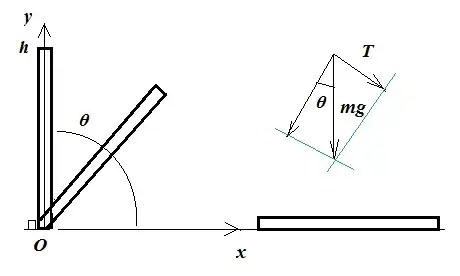
I was playing with a small ruler by repeatedly toppling it, see diagram below:
The ruler, standing $h$ tall and approximately a regular bar, is prevented from free-rotating by a fixed ridge (a book, usually) in point $O$ and then allowed to topple until it hits the $xz$-plane. My desk and the ruler both have quite smooth, hard surfaces and I can't help noticing that after impact the ruler slides along the surface in the $x$-direction for a bit until it is halted by friction.
This suggests the ruler had momentum in the $x$-direction, after impact with the desk's surface. But I can't work out where it comes from. Is some of the rotational kinetic energy the ruler acquired during toppling converted to translational kinetic energy on impact? If so, how?
The forces acting on the centor of gravity of the ruler are shown in the right hand top corner of the diagram. Obviously it's the moment $\frac{Th}{2}$ that's causing rotation around $O$ and the equation of motion is:
$$\frac{Th}{2}=I\ddot{\theta}.$$
With:
$$T=mg\sin\theta.$$
And:
$$\ddot{\theta}=\omega\frac{\mathrm{d} \omega}{\mathrm{d} \theta}.$$
So:
$$\frac{mgh}{2}\sin\theta \mathrm{d}\theta=I\omega \mathrm{d}\omega.$$
Integrated between $0,0$ and $\frac{\pi}{2},\omega$, we get:
$$K=\frac{I\omega^2}{2}=\frac{mgh}{2}.$$
$\frac{mgh}{2}$ is of course simply the amount of potential energy that has been converted to kinetic energy by lowering the CoG from $h/2$ to $0$.
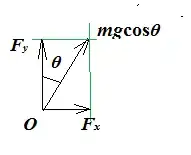
Now let's look at point $O$:
In $O$, $mg\cos\theta$ has to be countered to prevent the ruler from moving radially (from $O$ to the CoG or vice versa).
Decomposing we get:
$$F_x=mg\cos\theta \sin\theta.$$
But at $\theta=\pi /2$, $F_x$ vanishes, so it can't be that force that's responsible for any horizontal motion.
Clearly I'm missing something here, but what is it?