Amplitude of an electromagnetic wave containing a single photon

Question

Given a light pulse in vacuum containing a single photon with an energy $E=h\nu$, what is the peak value of the electric / magnetic field?

Answer 1

The electric and magnetic fields of a single photon in a box are in fact very important and interesting. If you fix the size of the box, then yes, you can define the peak magnetic or electric field value. It's a concept that comes up in cavity QED, and was important to Serge Haroche's Nobel Prize this year (along with a number of other researchers). In that experiment, his group measured the electric field of single and a few photons trapped in a cavity. It's a very popular field right now.

However, to have a well defined energy, you need to specify a volume. In a laser, you find an electric field for a flux of photons (n photons per unit time), but if you confine the photon to a box you get an electric field per photon. I'll show you the second calculations because it's more interesting.

Put a single photon in a box of volume $V$. The energy of the photon is $\hbar \omega$ (or $\frac{3}{2} \hbar \omega$, if you count the zero-point energy, but for this rough calculation let's ignore that). Now, equate that to the classical energy of a magnetic and electric field in a box of volume $V$:

$$\hbar \omega = \frac{\epsilon_0}{2} |\vec E|^2 V + \frac{1}{2\mu_0} |\vec B|^2 V = \frac{1}{2} \epsilon_0 E_\textrm{peak}^2 V$$

There is an extra factor of $1/2$ because, typically, we're considering a standing wave. Also, I've set the magnetic and electric contributions to be equal, as should be true for light in vacuum. An interesting and related problem is the effect of a single photon on a single atom contained in the box, where the energy of the atom is $U = -\vec d \cdot \vec E$. If this sounds interesting, look up strong coupling regime, vacuum Rabi splitting, or cavity quantum electrodynamics. Incidentally, the electric field fluctuations of photons (or lack thereof!) in vacuum are responsible for the Lamb shift, a small but measureable shift in energies of the hydrogen atom.

Answer 2

This is a reasonable question to ask, but the answer is probably not what you're expecting: the electric and magnetic fields don't have well-defined values in a state with a fixed number of photons. The electric and magnetic field operators do not commute with the number operator which counts photons. (They can't, because they are components of the exterior derivative of the field potential operator, which creates/annihilates photons.) The lack of commutativity implies via Heisenberg's uncertainty principle that the field might have arbitrarily large values.

Answer 3

@charles Fransis correctly points out that the expected value of the electric field is zero. (that is, $\langle 1|E|1 \rangle = 0$)

And to quote @user1504 (also stated by @vadim):

The electric and magnetic field operators do not commute with the number operator which counts photons. (They can't, because they are components of the exterior derivative of the field potential operator, which creates/annihilates photons.) The lack of commutativity implies via Heisenberg's uncertainty principle that the field might have arbitrarily large values.

So yes, we know that since the photon number operator doesn't commute with the E-field operator, so we know the E is uncertain. But realistically speaking, can a really photon have any arbitrarily high E-field amplitude? It could in the same sense that a bounded electron might appear on the moon because it's wavefunction has some tiny component.

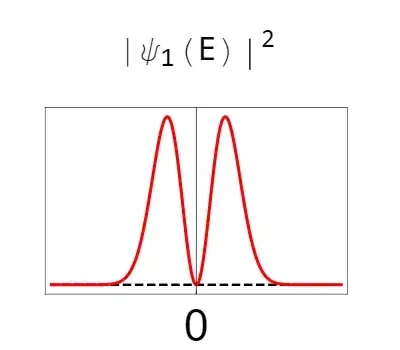
Putting things more precisely: what is the probability distribution associated with measuring a particular E-field amplitude for a single photon (that is what is $|\langle E|1\rangle|^2 = |\psi_1(E)|^2$).

The answer is that a photon has a very unique probability distribution that looks like this:

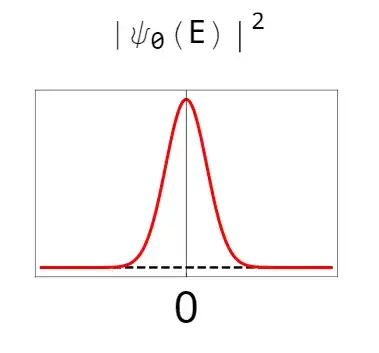
Which, for comparison to if there was only vacuum:

So here we can visually see how much of an electric field amplitude we really expect to see, with the vacuum as a reference. While the average value is zero, the absolute value of that amplitude is certainly larger than the absolute value of the vacuum and is around the FWHM (full width half max) of the vacuum distribution. (or eyeballing it, roughly double the value of the vacuum on average)

This is a very commonly measured feature of single photons (check out this paper for a classic take on it, and this for something more modern), and this probability distribution (when measuring a photon's electric field) is often used to identify if the quantum state of light is (or isn't) a "pure" single photon.

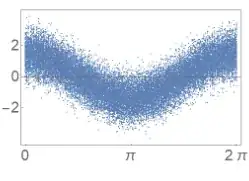
To see this more clearly, a coherent state, when looking at the statistics as the "phase" of the light changes, it would look like this:

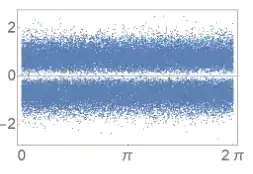
(which is basically $\cos(\omega t)$ with gaussian noise). By comparison a single photon state looks like this:

And here we see that changing a "phase" doesn't do anything to a "single photon" (which may have to do with single photons not having a well defined phase.)

Here's an example in the linked experiment:

(in this case the x-axis is TIME, not phase!) Pulses with a specific time delay are sent into a homodyne detector (which measures the E-field). Here you can see that for a specific temporal value associated with when the photon hits the detector (repeated for multiple measurements). The value of the electric field has a new distribution, and you see the dip at zero.

Answer 4

The electromagnetic field can be understood as the expectation $\langle A(x) \rangle$ of the photon field operator, $A(x)$, which annihilates or creates a photon in an interaction with an electron (or other charged particle), provided of course that a charged particle is present for the interaction to take place. For a single photon state $|\phi \rangle$ the action of $A$ will be to annihilate the photon, or create another one, meaning that the resulting state is a superposition of states with two or no photons. The inner product with a one photon state is zero and you necessarily have $$ \langle A(x) \rangle = \langle \phi | A(x) |\phi \rangle = 0. $$

Which answers the question. The amplitude of such a state is necessarily $0$. You only get a non-zero classical electromagnetic field $\langle A(x) \rangle$ (including a classical electromagnetic wave) from states which contain an indeterminate number of photons.

Equivalently, as @user1504 put it

The electric and magnetic field operators do not commute with the number operator which counts photons.

In other words, for a state with a definite number of photons, it is not meaningful to talk of the classical electric or magnetic field, or of a classical electromagnetic wave.

Answer 5

The amplitude of an electromagnetic wave does not commute with the photon number. A state with a single photon is an eigenstate of the photon number operator: $$ n_{\mathbf{k},\lambda}|1_{\mathbf{k},\lambda}\rangle=a^\dagger_{\mathbf{k},\lambda}a_{\mathbf{k},\lambda}|1_{\mathbf{k},\lambda}\rangle=|1_{\mathbf{k},\lambda}\rangle. $$ On the other hand, the states having a definite value of an amplitude (whether one talks about electric field, magnetic field or vector potential) are more like position and momentum operators of the quantum oscillator, corresponding to the given quantum mode, i.e., they do not commute with the number operator: $$ \hat{E} = E_0a_{\mathbf{k},\lambda} + E_0^* a_{\mathbf{k},\lambda}^\dagger $$ (see, e.g., the Wikipedia for the expressions for the coefficients $E_0$.) Thus, the number of photons and the amplitude of the field are related via the uncertainty relation: if one of them is measured, the other can have any value. More specifically: $$ \langle 1_{\mathbf{k},\lambda}|\hat{E}|1_{\mathbf{k},\lambda}\rangle=0,\\ \langle 1_{\mathbf{k},\lambda}|\hat{E}^2|1_{\mathbf{k},\lambda}\rangle= |E_0|^2 \langle 1_{\mathbf{k},\lambda}|2a^\dagger_{\mathbf{k},\lambda}a_{\mathbf{k},\lambda}+1|1_{\mathbf{k},\lambda}\rangle = 3|E_0|^2. $$

Answer 6

A single photon's wave could have different shapes, really, so the maximum of the Electric field would be impossible to compute given the parameters above. It could be really short with a very high electric field or really long with a low electric field. Or, whatever. That light comes in "chunks" as photons doesn't restrict you.

Suppose the energy of an ocean wave were hv... then how high is it? Well, it would depend on the width and other factors... as surf comes in waves so does light come in photons, but we wouldn't know the exact shape from the question.

Answer 7

The electric field of a single photon is found to be $E=\frac{hc}{2e\lambda^2}$ https://doi.org/10.1016/j.ijleo.2019.01.074

Answer 8

If an atom emits energy hf, it emits also an angular momentum (spin). That combination is called "photon" or "wave packet". Linking the appropriate formulas from QM and E&M waves, you get the diameter of the wave packet (about λ/2) but not the length. The radius and the direction of propagation do not change as long as the wave packet is not disturbed. It is not locked in a box but propagates in vacuum.

If the coherence length L is accepted as the length of the cylindrical wave packet, you can calculate the energy density u~f³/L and the electric field strength E~sqrt(f³/L), which is constant inside the cylinder.

I got the following results: a) The Hydrogen line at 1420 MHz has FWHM≈5 kHz, L≈60,000 m, E≈1e-8 V/m

b) The Sodium D-Line has FWHM≈10 MHz, L≈6 m, E≈220 V/m

c) X-ray, λ≈1e-12 m, L≈1000λ, E≈1e16 V/m

If you choose a different shape, perhaps like a cigar, those values differ

Answer 9

In a box of defined, thus finite, volume an infinitely long wave is by definition impossible. Positing an infinitely long wave would also deny the physical reality of the photon having a wavelength, as wavelength is never infinite; measured wavelengths, of visible light for instance, are extremely short, not infinite.

By defining the volume of the box, i.e. by setting a volume arbitrarily, one is in effect setting an arbitrary upper limit on wavelength. But a single photon cannot yield a value for wavelength, since there is no possibility of measuring a peak-to-peak distance between adjacent peaks in the waveform, when there is no second peak to measure to.

Energy is a derivative of amplitude, but only in a statistical sense, as an average of many photons per second, since the uncertainty principle makes measuring a single photon problematic. Its electric and magnetic field values are only a statistical average; individual photons may deviate widely from that average. Equations derived from these group averages are likewise valid only for the group, not for individual photons.