Producing photons with same frequency, different amplitude wave

Question

I don't understand how two photons of the same frequency can have different amplitudes, neither how to produce them.

I know that classically the square of the amplitude is proportional to the energy, but photons aren't classical particles.

My understanding is that a photon's energy is $h\nu$ - what does the square of its amplitude represent, then? Are there bounds to the amplitude of an EM wave?

Take two waves of amplitudes $A_1$ and $A_2$ and frequency $f_0$. If $A_2 = 2A_1$, can the wave with amplitude $A_2$ be said to carry/be two $A_1$ photons of frequency $f_0$?

Answer 1

Some of the other answers have suggested that the amplitude of the photon's wavefunction is well defined, and that it has the same value for any two photons of the same energy. Whatever else we may say, this can't possibly be right. The amplitude of an electromagnetic wave is defined either by its electric field or by its magnetic field. (In a sensible system of units, these two fields have the same units.) If this amplitude is the same for any two photons with frequencies of $10^8$ Hz, then what is this amplitude? There is no possible answer that makes sense on dimensional grounds.

There are two possible answers to this question, depending on how strict one wants to be.

(1) Strict answer: Photons don't have wavefunctions. See What equation describes the wavefunction of a single photon?

(2) Not-so-strict answer: In some contexts, you can get away with considering a photon to have a wavefunction. It is then possible to calculate its amplitude. The amplitude can be different for different photons of the same frequency. See Amplitude of an electromagnetic wave containing a single photon , which this question is basically a duplicate of.

Answer 2

Take two waves of amplitudes $A_1$ and $A_2$ and frequency $f_0$. If $A_2 = 2A_1$, can the wave with amplitude $A_2$ be said to carry/be two $A_1$ photons of frequency $f_0$?

Kind of like that. Replace the word "photons" with "quanta" and you'll be pretty close.

As you may know, the EM field can be broken down into components at various frequencies, or modes, each of which can store energy independently. The energy stored in a mode of frequency $f$ can only be a multiple of $hf$. That's all the formula $E=hf$ means. If an EM wave has energy $2hf$, then it has two quanta of energy at that frequency. These quanta are not the same as what we actually call photons, though. Whereas a quantum of energy is localized to a single frequency, a photon (as we usually think of it) is localized in position, and thus consists of excitations at many different frequencies.

The amplitude of the electric field of an EM wave is proportional to the square root of the energy density it carries. And since $E = nhf$ (per unit volume) for a single mode, a monochromatic EM wave will have an amplitude proportional to $\sqrt{n}$, the square root of the excitation number of that mode. But remember, excitation number is not the same as photon number, so it's not as simple as saying that the amplitude is proportional to the square root of the number of photons. That's just an approximation that works when the number of photons is large enough that you can treat the system classically.

Answer 3

If you insist on thinking of photons as waves (which is fine as long as you ignore absorption, though you should really think of it as a disturbance in an electromagnetic field), you can more or less think of all of their amplitudes as being equal, and this is why your premise doesn't make sense.

More precisely, the amplitude of a single photon isn't constant in space and time, but in a broad sense the "total amplitude" of all photons is the same, which I explain more below. It is important to remember that they are not some infinitely extending wave (which would imply infinite energy) but rather localized probability density which is a wave packet. This is the wave dual of the particle.

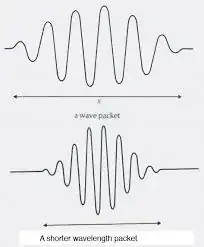
(A longer wave packet would have a smaller average amplitude, while a shorter one would have a greater amplitude, but the integral of the squared amplitude will always be 1)

And the amplitude of this wave does not even correspond to any observable quantity. In fact, according to schroedinger's equation, the amplitude of this wavefunction is not even a real number, but rather complex. However, the square of the amplitude IS something meaningful: probability density. When you are talking about individual photons (or any quantum particle), rather than thinking about energy intensity you should be thinking about the probability intensity of being here or there or being in a certain state. When you aggregate many photons together, the amplitudes of their superimposed probability densities would correspond in a sense to a real wave intensity on average, and that would be your connection to a classical idea of amplitude. But again, speaking of a single photon, an "intensity" doesn't really make sense.

The energy of a wave is proportional to the integral of the square of it's amplitude. (Note that it is not simply proportional to A^2. This would be the power, not the energy) This is why the energy of a wave packet of constant amplitude is proportional to the square of the amplitude. But this is not the case with a quantum wavefunction as it is a localized wave packet. Since this constant (the integral of probability of being anywhere in space) is always 1, the average or total square amplitude is constant for all photons so it does not appear in the equation for energy.

Comment on Ben cromwell's answer (sorry I can't comment):

@ben Crowell, while your answer is correct, I don't think it directly answers the OP's question. I want to point out that your second explanation is clearly the more relevant one and is at the core of what I was said in my answer. OP is starting with the concept that a photon can be thought of as a wave or wavefunction, which is true (although this comes with many caveats, the basic idea is true), and waves have amplitude. The key thing we agree on is that the amplitude is not constant over space or even for a given photon wavefunction as it depends on boundary conditions. This is exactly my point: since it must obey normalization, you can think (very roughly) of it's "total amplitude" as being constant and this is why it doesn't affect total energy.

Answer 4

I am making this an answer because it is too long for comments and in a sense does answer with a reference.

This is a wrong idea of photons that you have:

I don't understand how two photons of the same frequency can have different amplitudes, neither how to produce them.

Two photons of the same frequency have the same "amplitude", since the only thing they have to differ from each other is frequency. Otherwise they are identical. They are the quantum substructure of classical electromagnetism. The macroscopic electric field of a wave consisting of photons does have an amplitude which is statistically built up from the individual photons.

@Lubos Motl has an extensive article of how classical fields are built up from the quantum substructure, and mathematical ability is necessary to understand it. As @dmckee says wave packets come in.

But he also uses the electromagnetic field in a simple example.

The electromagnetic example starts at this paragraph:

However, in the rest of this section, I want to focus on another way how to see classical physics of fields emerge out of large ensembles of photons, one that mimics the thermodynamic limit of statistical physics (even in the context of classical mechanics).

Answer 5

Here is a simple calculation to think about. Imagine a generic radio transmitter emitting, say, 1 watt. That's 1 joule/second. Suppose the frequency is 100 MHz. Take the Einstein relation E=hf, where h is Planck's constant. Figure out the flux of photons (number emitted per second). To speak of photons in a QM sense the number of photons needs to be relatively small. The sea of photons emitted by our transmitter behave collectively as a wave: in effect a Bose-Einstein condensate.