Intuition - why does the period not depend on the amplitude in a pendulum?

Question

I'm looking for an intuition on the relationship between time period and amplitude (for a small pertubation) of pendulums. Why does the period not depend on the amplitude? I know the math of the problem. I am looking for physical intuition.

Answer 1

The higher you are, the greater the maximum velocity and maximum potential energy.

Consider one pendulum lifted higher than a second both released at the same time. When the higher pendulum reaches the starting point of the second, it already has a velocity greater than 0.

This higher velocity allows the higher pendulum to complete its swing in the same amount of time as the lower, even though it has a longer path.

Since I'm at a computer now I will address a majority of what is said in the comments. For starters, this does not exactly apply to pendulum; only approximately, and the approximation gets worse as $\theta$ increases.

A good way to visualize this is through the Tautochrone curve which is a frictionless curve where for all heights, the time to fall is the same (this is the equivalent of a pendulum period if you ignore the backswing, or have 2 of these curves mirrored; which will be a perfect mirror of the front swing if energy is conserved in the system).

In this scenario, the accelerations work out perfectly (under the same gravity) so that they all arrive at the same time. This is unlike the circular motion, which is only approximately correct for small angles. The interesting thing to note is that looking at a small displacement of a tautochrone curve; it looks approximately circular if you only look at a small section near the bottom. This is an intuitive way to explain why a circular pendulum approximately has this behaviour with small angles.

(Henning mentioned a tautochrone curve in his answer as well. It seemed to be an appropriate way to add more intuition to this)

Answer 2

Hand-wavy intuition: Suppose we don't know about pendulums but want to construct a one-dimensional path, such that a point mass constrained to this path can oscillate around a low point with different amplitudes but constant period.

We do this from the bottom up -- so imagine that we have constructed the path from an altitude of $h_1$ down to $0$ and back up to $h_1$ on the other side. Now we want to extend that up to a sligher higher altitude $h_2$.

When we release our point mass at $h_2$, we can compute what its kinetic energy (and therefore its speed) will be at any altitude, so we can (at least in principle) compute how long it takes it to pass by the already made $h_1$-to-$h_1$ segment. This will be less time than our desired period, and half of the remaining time will be how long the point mass should take to move from $h_2$ to $h_1$. If that is sufficient time (that is, more than it would take the mass to fall straight down from $h_2$ to $h_1$), we can adjust how long time it takes, simply by making the section from $h_2$ to $h_1$ a suitably inclined plane.

Taking this process to the limit (where $h_2$ is just infinitesimally higher than $h_1$) we get some horrendous continuous-delay differential equation that I don't care to either derive in detail or solve -- but Huygens did it in 1659 and found that the solution is an inverted cycloid.

So if we have a bob gliding frictionlessly along a cycloid, it will indeed have the same period for any amplitude.

A pendulum, of course, swings in a circle rather than a cycloid -- but the cycloid turns out to be smooth enough (with nonzero but finite curvature) at the bottom that it can be approximated by a circle. This approximation is good enough that the difference in period between the circle and cycloid go to $0$ as the amplitude goes to $0$.

Answer 3

For small angular displacements, the pendulum differential equation is effectively linear and as such, the amplitude of the oscillation must be independent of the period. Why?

For a linear system, if $x_1(t)$ and $x_2(t)$ are two independent solutions, then $x_3(t) = a_1x_1(t) + a_2x_2(t)$ is also a solution (superposition property).

And so, if a linearized pendulum has a sinusoidal solution $x_1(t) = \cos(\omega_0 t + \phi_0)$, then $A\cos(\omega_0 t + \phi_0)$ is also a solution by the superposition property.

Answer 4

Here's an intuitive and non-rigorous answer.

By conservation on energy you can deduce that the pendulum will be moving more slowly when it has a smaller amplitude since it has a smaller change in height and so a smaller change in kinetic energy.

With smaller amplitudes the pendulum does not have as far to travel to complete a complete swing but it is also moving more slowly. The two effects cancel each other out (at least if the amplitude of vibration isn't too large).

Answer 5

The short answer is that a periodic function still has the same period if you scale it, so a linear differential equation with solutions of a given period has such solutions at any amplitude. The angle $\theta$ of a pendulum from the vertical satisfies $\ddot{\theta}=-\frac{g}{l}\sin\theta$, but for small angles we can replace $\sin\theta$ with $\theta$, giving an approximately linear equation of motion.

Answer 6

You can say it's because average speed (in the RMS sense) scales in the same way as displacement does: double the amplitude, and the RMS speed will also double. (To first-order approximation at least.)

Why would that be? Well, it's because average acceleration also scales proportionally, as that simply depends on the force. It's the particular feature of the harmonic oscillator that force depends linearly on displacement.

Answer 7

One possible approach to explain why the period does increase with initial angular starting off point is to imagine a pendulum where the string is made of taut wire. Imagine setting the initial angle at exactly $\pi$ radians. In this case the pendulum is in exact equilibrium and you may then say that the period is infinite. Now, you'd expect the relationship between the period and the starting angle to be monotonic, and since it starts off small for small angles, if the period increases from something small to infinite, at in-between starting angles you'd expect the period to get larger as the starting angle increases.

For small enough angles, this monotonic function presumably is flat, meaning that period is roughly independent of initial starting angle.

Answer 8

The larger the swing, the more vertical is the angle at which the pendulum bob starts falling at, hence the faster it accelerates at the start, and the increase in speed exactly balances the longer swing length.

Just read Enn's answer in more detail, and my answer is, more or less, a more intuitive presentation of his. The best answer is to combine his and mine: larger acceleration at start due to increased angle, and larger fall distance, hence faster movement.

Answer 9

I wrote this answer as a response to this question but as it was marked as a duplicate I add to the answers here.

The most important thing is that the acceleration (and hence the force) is proportional to the displacement from a fixed point.

Suppose that we start with a displacement of $A$ from a fixed position with the object at rest.
Let the acceleration of the object at this position be $KA$ where $K$ is a constant which would be $\dfrac{\text{spring constant}}{\text{mass}}$ for a spring mass system or something equivalent for a simple pendulum.

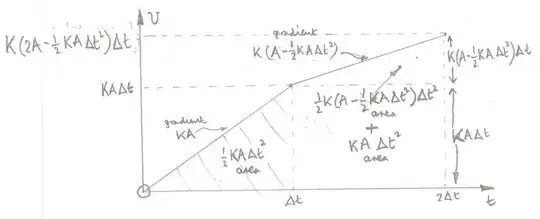
Below there is a velocity against time graph to illustrate the motion of the object from $\rm time = 0$ to $ {\rm time} = 2 \Delta t$.

In the first interval the acceleration is approximately $KA$ the change in velocity is $KA\Delta t$ and the displacement of the object is approximately $\frac 1 2 KA \Delta t^2$.

In the second interval the acceleration is approximately $K(A-\dfrac 12 KA \Delta t^2)$ the change in velocity is $K(A-\dfrac 12 KA \Delta t^2)\Delta t$ and the displacement of the object is approximately $\frac 1 2 K(3A-\frac 12 KA\Delta t^2 )\Delta t^2$.

One could continue but the key feature is already there.

Noting that $K$ is a constant of the motion, the displacement in each successive interval of time is proportional to the initial displacement $A$ which is the amplitude of the motion.

If the amplitude doubled so would the distance covered in a given time.

Thus the period of the motion does not depend on the amplitude.

This analysis shows that for the amplitude to be the common factor in successive displacements there must be a linear relationship between the acceleration and the displacement.