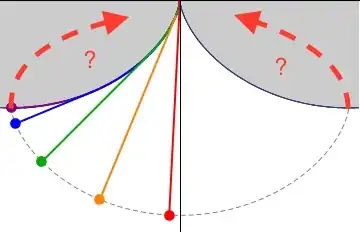
This sketch became too long to be a comment so I will post it as an answer anyway.
Let us say we have a wire forming a cycloid in the vertical plane as in the figure bellow
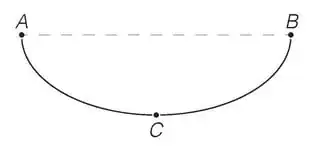
A friction-less bead into this wire will oscillate with known period $T$ independently of its releasing point. Assume we can symmetrically continue the wire above the dashed line. If we release the bead from $A'$, which is infinitesimally close to $A$ but above the dashed line, then it will take a time $\Delta t_{AB}<T$ to complete the segment ${AB}+BA$ since it travels faster. If we want the same period $T$ for the bead to oscillate between $A'$ and $B'$, then the time taken along $A'A$ shall be $d t_{A'A}=(T-\Delta t_{AB})/2$. The idea is to use energy conservation and the parametric equation of the cycloid to compute $\Delta t_{AB}$ and then obtain $d t_{A'A}$.The last step is to suitably chose the slope of the straight segment $A'A$ so that the interval $dt$ for the bead to slide from $A'$ to $A$ matches $dt_{A'A}$. I think you will find that $dt_{A'A}<dt$ even when $A'$ is vertically above $A$ (which gives the least $dt$). This means that the tautochrone curve cannot be continued above the dashed line. You can also recall that this construction can be actually used to obtain the tautochrone. The slope of the infinitesimal segments are always increasing, from zero at $C$ to $\pi/2$ at $B$. One increment further and we can no longer increase the slope.