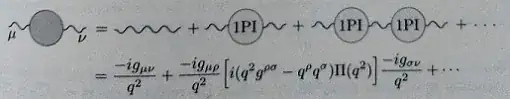How to correctly understand these "1-particle-irreducible insertions"?

Question

In QED, when dealing with the vacuum polarization and the photon propagator, some authors like Peskin & Schroeder introduce the so-called "1-particle irreducible" diagrams. These are defined as:

Let us define a one-particle irreducible (1PI) diagram to be any diagram that cannot be split in two by removing a single line.

So this is a "graphical definition", so that given a diagram we determine whether it is a 1PI or not by looking at whether or not a line can be removed leaving two diagrams that make sense by themselves.

That much I understand. What I don't understand is that Peskin & Schroeder then does the following: consider the 1-loop correction to the photon propagator. That would be the vacuum polarization diagram.

The authors denote its value by $i\Pi_2^{\mu\nu}(p)$. They then define $i\Pi^{\mu\nu}(p)$ to be "the sum of all 1PI insertions into the photon propagator". This is ilustrated by eq. (7.72)

Then they say on the bottom of p. 245 that the exact two point function is

Now I don't understand what he is doing here. For example, he claims that for $\Pi^{\mu\nu}(q)$ the Ward identity holds $q_\mu \Pi^{\mu\nu}(q)=0$.

My question is:

1. What is the motivation for defining this $\Pi^{\mu\nu}$, namely to consider that "1-particle-irreducible insertions"?

2. How do we deal mathematically with that? Because I just have one "pictorial" definition of what a single 1PI is, I have no idea what it actually means to consider "all possible 1PI insertions", and this confuses me.

3. Why the full dressed propagator which is defined as the Fourier transform of $\langle \Omega |T\{A^{\mu}(x)A^{\nu}(y)\}|\Omega\rangle$ is expanded as that sum? The author doesn't seems to prove that.

Edit: Based on the answers I was thinking and I believe the point is that in the last equation the second term on the RHS is the sum over all 1PI's, the second is the sum over all diagrams with two 1PI pieces and so forth.

But it seems the author implies that: "the sum over all diagrams with two 1PI pieces is the same as the product of two sums of all 1PI's". Namely, I think the author is trying to write down the following (writing $G_0^{\mu\nu}$ for the bare propagator).

$$G^{\mu\nu}=G_0^{\mu\nu}+G_0^{\mu\alpha}\Pi_{\alpha\beta}G_0^{\beta\nu}+G_0^{\mu\alpha}\Pi_{\alpha\beta}G_0^{\beta\rho}\Pi_{\rho\sigma}G_0^{\sigma\nu}$$

now I've tried to understand why the "sum over all diagrams with two 1PI pieces" is actually that, but I think I don't get it.

Let two diagrams be given that are decomposed in two 1PI pieces each. The first diagram has 1PI pieces with values $I_{\alpha\beta}$ and $II_{\alpha\beta}$ while the second has values $I'_{\alpha\beta}$ and $II'_{\alpha\beta}$. Summing them we have

$$G_0^{\mu\alpha}I_{\alpha\beta}G_0^{\beta\rho}II_{\rho\sigma}G_0^{\sigma\nu}+G_0^{\mu\alpha}I'_{\alpha\beta}G_0^{\beta\rho}II'_{\rho\sigma}G_0^{\sigma\nu}=G_0^{\mu\alpha}(I_{\alpha\beta}G_0^{\beta\rho}II_{\rho\sigma}+I'_{\alpha\beta}G_0^{\beta\rho}II'_{\rho\sigma})G_0^{\sigma\nu}$$

now I can't reduce this to something with $I+I'$ and $II+II'$ which I think is what I need. What is wrong in my reasoning?

Answer 1

1. There isn't really much of a motivation except that it's useful.

2. There's really not much to deal with: You have the set of all Feynman diagrams. You define that a 1PI diagram is one that cannot become two non-trivial separate diagrams by cutting a single line. So each diagram that is not 1PI has such a line. The two pieces you get after cutting the single line are either 1PI or not, if not, you repeat the process. This decomposes every diagram as a string of 1PI diagrams, so the set of all diagrams is the union of "1PI diagrams", "2 1PI diagrams connected by a line", "3 1PI diagrams connected by a line", and so on. Saying one considers "all possible 1PI insertions" in the propagator simply means one considers the sum over all 1PI diagrams with two external legs.

3. There's nothing to prove, really. You start from knowing that the dressed propagator is the sum over all diagrams, and since the strings of 1PI diagrams exhaust all diagrams, you can write the sum over all diagrams as the sum over 1PI diagrams plus the sum over all 2 1PI diagrams plus the sum over all 3 1PI diagrams and so on. This expansion is useful (as you will probably see shortly in the text you're reading) because it yields a geometric series in the 1PI contributions, which then lets us conclude that the 1PI contributions are precisely the mass shift between the bare and the dressed particles.

Answer 2

The point of defining the 1PI diagrams is that calculating all the diagrams (including the reducible ones) is redundant. Say you already calculated the lowest order for the self energy, the diagram with an electron loop. What if you have an electron loop and then another electron loop (so a bit like your second picture)? Is that any harder? No, it's just the value of one electron loop squared. So if we just calculate the 1PI diagrams we can get all the diagrams with very little extra work.

All possible 1PI insertions just means that, that inside of the shaded circle you can put anything as long as it connects with the external lines and it's 1PI. The pictorial intuition is a good intuition, because, again, the point of the 1PI diagrams is to simplify. If a diagram can be separated in half by a single cut, then it's just the product of two simpler diagrams.

As for the propagator, recall that earlier in the book you calculated the two point function for the scalar field and it turned out to be the sum of all diagrams with two external points at fixed positions $x$ and $y$. The Fourier transform is just the momentum space version of that. And the sum of all possible diagrams with two external photons is what P&S draw in the second picture, by definition of 1PI: if some diagram is not 1PI, it can be separated into two 1PI pieces.

In regards to your edit: what the book claims is only true if you include all diagrams at a given order. In your example, you've missed that you should also have a $I'-II$ and a $I-II'$ diagram. The sum of all four will give what you want.