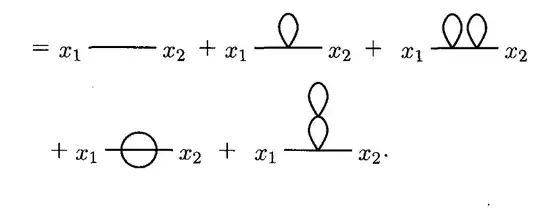What is the precise definition of a $n$-loop one-particle irreducible ($1$PI) diagram?
For example, consider the following diagrams.
- Is the first diagram a $0$-loop $1$PI diagram?
- Is the second diagram $1$-loop $1$PI ?
- Is the third diagram $2$-loop $1$P (i.e. reducible)?
- Are the fourth and fifth diagrams $2$-loop $1$PI?