How do we calculate the irradience of an EM wave?

Question

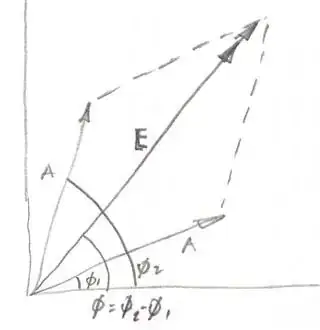
I've been told that the Irradience = time average of the electric field squared. However, I've also been told that it's equal to the total Amplitude of the electric field squared. I'm kinda confused as to which interpretation it is.

There are 2 calculations for the irradience which have given me 2 different values.

The first is done via an algebraic method:

$$E_\text{tot} = A\cos(\omega t + \phi_1) + A\cos(\omega t + \phi_2)$$ $$=2A\cos(\frac{\phi_1 - \phi_2}{2})\cos(\omega t + \frac{\phi_1 + \phi_2}{2})$$ $$= 2A \cos(k\frac{r_2-r_1}{2})\cos(\omega t - k\frac{r_1 + r_2}{2})$$ If we were to take the time average of the electric field squared in this case, we would end up with Irradience being equal to: $$=\frac{1}{2}A^2\cos^2([k\{r_1 - r_2\}]/2)$$

This is clearly not just the total Amplitude squared.

However, if we were to now preform these calculations via complex notation:

$$E_\text{tot} = A_1e^{i(\omega t + \phi_1)} + A_2e^{i(\omega t + \phi_2)} = (A_1e^{i\phi_1} + A_1e^{i\phi_1})e^{i\omega t}$$

Now, if we were to find the irradience, it would end up being equal to the total amplitude squared.

Why is this the case?

Answer 1

Strictly speaking, irradiance is an energy flux per unit area. The flux of an electromagnetic wave is given by the Poynting vector: $\mathbf{S}=\mathbf{E}\times\mathbf{H}$. As both electric and magnetic field are time dependent, the flux is time-dependent.

The catch is that the frequency of electromagnetic field is very high in most practical applications - e.g., $\sim 10^{15}$Hz. Most measurement devices do not respond in $10^{-15}$ fraction of second - they perform "averaging" over many periods of the field. It is crucial here that they respond to the magnitude squared of the field, since average of $\cos(\omega t)$ over many periods tends to zero, but average of $\cos^2(\omega t)$ becomes $1/2$. (See Explanation of pattern produced by Interferometers for a more detailed example of such an averaging.)

The reasons why most detectors are quadratic is that:

• in quantum terms, the rate of transitions between energy levels is proportional to the matrix element of coupling to the EM field, which is proportional to the magnitude of the field.
• in classical terms detection is performed using a diode or another non-linear element (see, e.g., the diagram in How is an LC oscillator used for generating signals? and Quantum description of radio antenna.)

Thus, most practical discussions of flux would deal with a quantity averaged over the period of oscillations, without getting in the details of how this averaging is done. (Note that we use the same convention for for discussing the everyday electricity - the 110/220V designations for power grids correspond to an effective dc current that would produce the same power output as the actual ac current in the grid.)

(image source)

Answer 2

You find the resultant amplitude and then square the result.

If at a position you have two waves of amplitude $A$ which are in phase with one another the irradiance is proportional to $(A+A)^2 = 4A^2$ not $A^2+A^2 = 2 A^2$.

Each wave alone would produce a "displacement" and then you use the principle of superposition to find the resultant "displacement".
Finally you square the "displacement".

Your two equations are equivalent and the addition for both can be represented by the diagram below.

$E^2 = A^2+A^2+2AA\cos \phi = 4A^2 \cos^2 \frac \phi 2$