Lets take the following example
According to above examples it means that velocity at the above portion is max while the velocity at lower portion is min.
But I think it should be the same at both parts (just opposite in direction).
Why are both different?
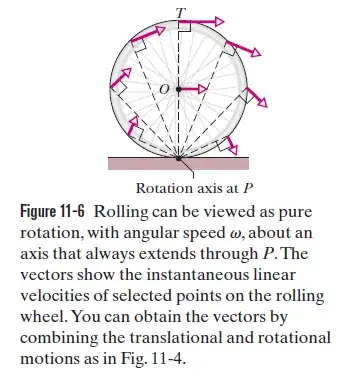
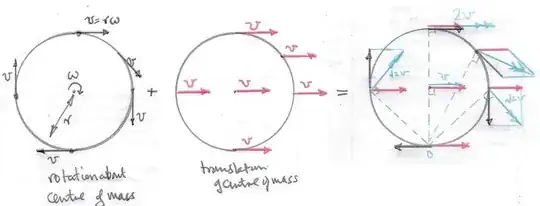
You have to remember that the entire wheel is also moving.
Think of this. Where the wheel meets the ground, the velocity of the contact point must be 0, otherwise the wheel would be skidding. Another way of looking at it is that at the contact point the forward velocity of the wheel is cancelled by the backward velocity of the point. On the other hand, at the top of the wheel these velocities add together: the velocity of the entire wheel with respect to the ground, plus the velocity of that point with respect to the centre of the wheel.
I once tested this, when I drove behind a truck that was trailing a rope on the road. I drove one of my front wheels over the rope and instantly the rope broke. It had to break because one end of the rope was moving at the speed of the truck, while the other was stationary between the road and my tyre.
In the no slipping condition the translational speed $v$ of the centre of mass of the wheel and the angular speed of rotation $\omega$ of the wheel are related.
$v= r \omega$ where $r$ is the radius of the wheel.
So one can find the vector sum (blue) of the translational velocity of the wheel at any point (red) and the tangential velocity of the wheel at any point (grey) as in done in the diagram below.
Since at the instant shown on the right hand diagram the wheel is roating about the point of contact the directions of those resultant velocities at each point on the wheel must be at right to the line joining the point to the point of contact between the wheel and the ground (green).
There are two contributions to the speed for which the spokes on the wheel move at. There is translational velocity and rotational velocity.
On the top part of the wheel the vectors corresponding to the translational and rotational velocities add together as they are moving in the same direction (to the right).
Whereas at the bottom section the wheel is rotating in the opposite direction to which the wheel is moving along (as the bike moves); in other words the vector corresponding to the rotational velocity is to the left, but the bike and hence the wheel is moving towards the right. So these two vectors subtract.
This is why the top section is moving faster than the bottom.
Rotation about P is equivalent to rotation about O plus translation of O horizontally. This works in reverse to. Any rotation + translation can be described equivalently by a pure rotation about a distant point.
Let's place a coordinate system at P and measure the linear velocity at an arbitrary point $\vec{r}$.
$$ \vec{v} = \vec{\omega} \times \vec{r} $$
You should be able to imagine this, but if it gives you trouble, use an actual tire, or any flat circular object of reasonable size. Perhaps a lid for a storage container, or a plate (something like a coin is much to small).
Think of it this way:
People. Please. All parts of a rotating disc travel at EXACTLY the same speed dependent upon ONLY the distance from its center. The top is NOT moving faster than the bottom--it just looks like it is due to camera blurring--an unintentional photographic effect. If the spokes were traveling at different speeds the wheel would NECESSARILY deform or disintegrate. We have some great attempts to interpret, explain and prove the original thesis--but such proof is itself an illusion based on misinterpretation by some otherwise EXTREMELY intelligent people. If the original conjecture is correct then, again necessarily, THE EARTH ITSELF WOULD DISINTEGRATE. Velocity = 2 Pi * r (from the center) * rotational speed, at EVERY POINT OF THE WHEEL. If you look closely at the photo, the spokes appear bend around rim and at a varying degree everywhere. And I know that on stackexchange someone will call me an idiot. I'm cool with that. :P
