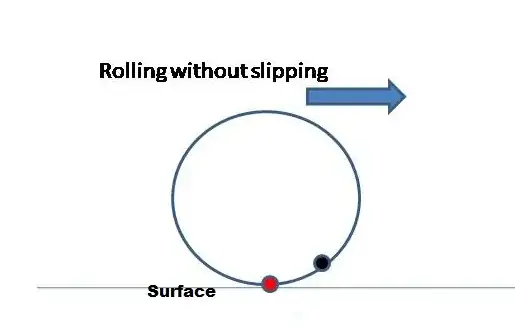
I was having a hard time to understand that the point of contact in case of rolling without sliding has zero velocity. So after some research, I posted my understanding as an answer How can the contact point of the rolling body have zero velocity? . But a new question arises and it this:
What will be the horizontal and vertical velocities of the black point at this moment of time when the red one is the point of contact?
My intuition says that the black point will also have zero horizontal velocity ( since it is a rigid body, all the points move in sync. So if red is at rest horizontally, all the points should have the same zero velocity in the horizontal direction), but some non-zero vertical velocity ( how much ?)
Thanks in advance for your comments and answers.