How can the contact point of a body rolling without slipping have zero velocity?

Question

They say that for a rolling body, the velocity of the contact point is zero. I'm not getting this. How can it be zero when it's in continuous motion?

Answer 1

What luck! Just yesterday I was thinking about this exact same phenomenon whilst watching the film 'The Imitation Game'; the title sequence contained a moving tank.

When I was little, I used to observe this all the time; not in wheels however, but in caterpillar tracks:

Notice how, when a segment of the track touches the ground, it just stays there, in exactly the same spot? Obviously, its velocity must therefore equal 0, as it contacts the ground.

It was not until more recently though that I extrapolated this feature of caterpillar tracks to wheels; a wheel is just a squished together caterpillar track, if you start with a caterpillar track, and continue reducing its length, you'll eventually have a wheel.

Because any point on a caterpillar track of any size is stationary when it contacts the ground, the single point on a wheel must also be stationary as it contacts the ground.

So, the wheel is constantly moving, but the points on it accelerate, decelerate, stop, start, at different times and at different rates.

Answer 2

The wheel is moving all the time, but each point on its circumference accelerates and decelerates all the time and when it is in contact with the ground it stops.

You can have a clear and convincing explanation watching this animation showing how each point on the wheel describes a cycloid

update

But remember that the ever-changing acceleration of each point is just an illusion created in the frame of reference of the road, which is at rest. This is due to the fact that the value $k$ of the translational forward-velocity of the wheel $k$ coincides with the circumference of the wheel $ k = 2\pi r\rightarrow v_w = 2\pi r $ m/s:

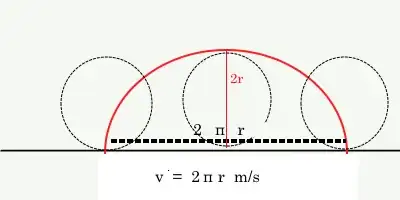
If you can, just imagine the car moving at the same speed and the wheel spinning at the same angular velocity but not touching the ground. Or imagine the wheel of a landing plane: as soon as it touches the ground the wheel synchronizes itself to $v= 2\pi r$ m/s.

--

^{An illusion of a completely different kind can be experienced by stroboscopic (or wagon-wheel) effect**}

Answer 3

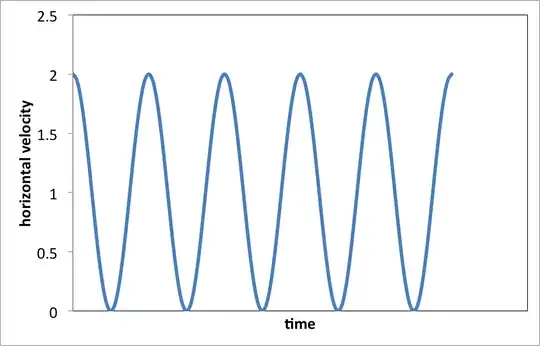
Consider a point $P$ on the surface of the wheel. If you look at the horizontal velocity of that point in the frame of reference of the wheel (axis stationary), then for a wheel of radius $r$ with angular velocity $\omega$ that point will have horizontal component of velocity

$$v_h = r\omega\cos(\omega t)$$

The linear velocity of the wheel $v = \omega r$. If we add those two velocities together, we find that the horizontal velocity in the frame of reference of the road is

$$v = r\omega\left(1 - cos(\omega t)\right)$$

That equation shows that the velocity will be exactly zero at the point where the wheel touches the road. The graph of that equation looks like this:

The position of the wheel over time (X,Y coordinates) will end up looking like this:

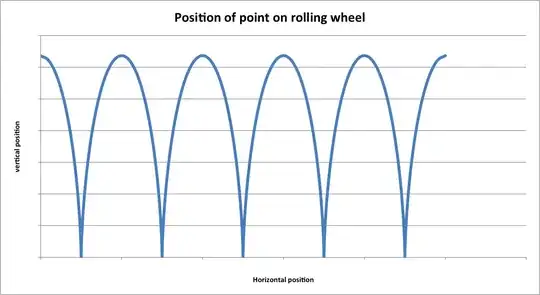
Both pictures should convince you that the point on the wheel really does stop momentarily.

Answer 4

you wrote: "How can [the velocity of the contact point] be zero when it's in continuous motion?".

However, you should keep in mind that motion is relative and therefore your question should be actually read as: "How can the velocity of the contact point be zero relative to the contact surface, when it's in continuous motion relative to its axis of rotation?" (for example, the axis of a rolling wheel).

But that is the nature of the principle of relativity; an object can be moving relative to one object and stand still relative to another.

imagine you are driving your car on the highway; your friend in the passenger seat is moving at the same velocity as you; from your point of view your friend is not moving at all; his velocity relative to you is zero, but relative to the road he "in continuous motion"; how can that be?

Answer 5

To me, this is most easily seen with the teeth of a gear that is running a conveyor belt.

This is basically the optimal non-slipping wheel; it rotates, and moves along the conveyor belt (really the belt moves along the wheel, but you can imagine the opposite). Each time a tooth enters the conveyor belt's track, the wheel effectively pivots on that tooth. Clearly, for a non-negligible period of time, the point at the end of tooth has no horizontal velocity, while the wheel is pivoting about it.

Answer 6

This answer is very simple and should completely clear your doubt:

When a body rolls on a horizontal surface without slipping the horizontal velocity of the contact point is zero. This is true not only for horizontal surfaces but any surface where the body rolls without slipping.

When does a block placed on a surface has a velocity with respect to the surface?
When it changes its position on the surface. If I push the block it will slide and change its position and so the block will move with respect to the surface.

Same applies for the contact point in rolling without slipping. If the contact point slips, it has velocity with respect to the surface. Hence, in rolling without slipping, the contact point touches the surface but never slips on it and hence no motion with respect to the surface which means the point of contact is always at rest with respect to the surface at the instant it touches the surface. See this.

Answer 7

An intuitive way to think about this is to imagine the wheel falling with the point of contact as the pivot. To exaggerate this intuition imagine a "wheel", which is an equilateral triangle rolling by falling about a vertex before rising about the next vertex and falling again. As it is rising and falling about a vertex, the vertex is stationary with respect to the surface.

Of course, in the case of the a circular wheel, the wheel only "falls" with respect to the point of contact only instantaneously to be replaced as the pivot by the "next" point on the wheel.

Hope this helps.

Answer 8

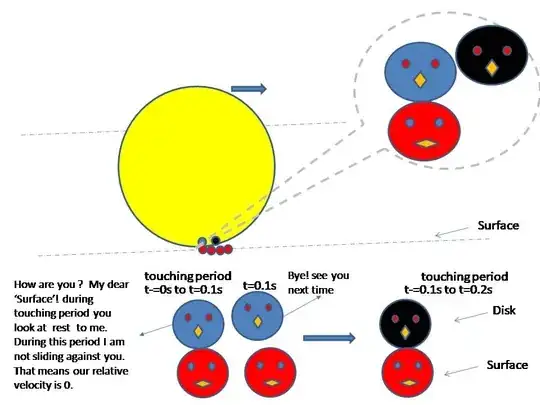
I am trying to develop an analogy since I also find it difficult to understand.
Imagine we have microscopic aliens hiding in two points; one on the surface of the disk (blue) and rest on the surface itself(red ones). From t=0 to t=0.1s there is a touching period. During this period they are having a casual talk and they observe that they are at rest wrt each other. They are not sliding. That means their relative velocity is 0. Once this touching period is over, the blue point detaches, and the next point of the disk(black) makes a contact with a new point(red) on the surface.

The confusion arises because we tend to observe all the points instead of just the contact point and find it difficult to understand how can the contact point be at rest. Another point is that the friction will still there because the blue point is pushing the red point backward, so a force in the form of friction appears which is in the direction of motion of the disk (Newton's Third Law).

Answer 9

I give a counterexample: a cog. Cogs cannot slide past each other, because the teeth are preventing that. Sliding motion is what's meant here.

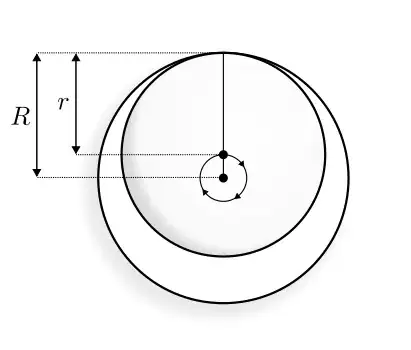
The point of contact is not actually a physical thing. It can therefore move arbitrarily fast. The same way that the spot of a laser pointer on the moon could travel faster than the speed of light. To see why this is true in this case, imagine a spirograph (picture below). We'll show that the contact point can move at arbitrarily high velocities, while everything physical (the mass) still moves at a finite speed.

The center of mass of the inner disk moves around a circle of radius $R-r$. Let's define $a=R-r$ for convenience. If we call the period $T$, the center of mass travels a distance $2\pi a$ in time $T$, so it moves with velocity $2\pi a/T$. The fastest point of the disk is the point opposite the contact point, which moves twice as fast as the center of mass at $4\pi a/T$. The contact point travels around the big circle in time $T$, so it moves with velocity $2\pi R/T$.

We now want to take the limit $a\rightarrow 0$. To do this the right way, I will fix the velocity of the COM to be $v_0$: $$v_0=2\pi a/T.$$

I will now express the contact point velocity in terms of $a$ and $v_0$: $$v_{cp}=\frac{2\pi R}{T}=\frac{ Rv_0}{a}$$

Finally, we can let the space between the inner disk and the outer rim grow arbitrarily small, i.e. let $r\rightarrow R$ or let $a\rightarrow 0$. In that case the velocity of the contact point grows arbitrarily large, while the velocity of the fastest point of the disk stays constant at $2v_0$. So I have proven my point.

We have one problem still when executing this experiment. The centripetal acceleration of the center of mass goes as

$$F=\frac{mv^2}{r}=\frac{mv_0^2}{a}$$

So we also have to provide arbitrarily large forces to do our experiment. We can (partly) solve this by picking $R$ large and by having a lightweight disk. Or perhaps by replacing the inner disk with a thin ring.

To conclude, the point of contact is ficticious in the sense that it can move without something physical being moved. It could potentially go faster than the speed of light. This means there is no problem with the relative velocity being zero at the contact point.

Answer 10

You're looking for velocity of points on the wheel's circumference with relation to the ground. Imagine that at each instant, each point on the circumference is connected to the point of contact by a "lever" which is a chord of the circle that forms the wheel. At point of contact the "lever" has zero length - in other words it is the only point on the circumference of the wheel that is not on the end of a "lever".

If you've ever used a throwing stick to hurl a ball for your dog to chase, you know that the length of the throwing stick increases the velocity of the ball significantly over what you can manage with your arm alone. Likewise, the longer the chord that attaches a point on the wheel to the ground, the greater that point's velocity. The longest "lever" is the chord which forms a diameter of the circle. Therefore, the point on top of the wheel has the greatest velocity. The point of contact is connected to no "lever" at all. Therefore, it is NOT being "thrown", and its velocity must be zero!

Answer 11

Have less than 50 rep, so can't write these in comments:

The question is phrased "How can it be zero when it's in continuous motion?"

@terry's answer is essentially: From the point of view of the surface (that the body rolls on), the motion of given points on the body's circumference is not continuous. Their velocity lowers until the time of contact, at which time the velocity is zero.

Adding to terry's answer: The velocity is zero for only an instant, a "point in time", immediately after which the velocity becomes non-zero again. "Intuitively" speaking, you could say that the point never stopped because it never "took the time to be in one place for some length of time". Mathematically it did stop, had zero velocity, for a moment.

Note that depending on the shape of the rolling body, there might be more than just a single point that stops. For example, for a rolling square, the whole lower side stops.

@Volker Siegel: From the perspective of the rail, the wheel is turning arount the contact point, which is at the top of the rail. Train wheels have a flange, whose edge protrudes a few centimetres below the top of the rail. When the wheel turns, for a brief time the lowest point on the flange moves backwards.

Answer 12

A planar body moving along a single axis has two degrees of freedom. Translation of the center and rotation about the center. The combination makes each part of the body to have different velocities according to the rule $$\vec{v} = \vec{v}_{cm} + \vec{\omega} \times \vec{r} $$

Rolling by definition is motion where the velocity at the contact point is zero (or no slip condition). When taken by component the above relationship becomes the scalar equation $v = v_{cm} + r \omega$. The rolling condition is $v=0$ so only movement where $\omega =-\frac{v_{cm}}{r}$ will produce pure rolling.

Answer 13

They say that for a rolling body, the velocity of the contact point is zero.

Indeed. In other words, as indicated in several other anwers already:
Any particular point (or smallish piece of surface) of the wheel which, at some particular instant, makes contact with the pavement has vanishing instantaneous speed with respect to the pavement, at that instant. (Otherwise we'd say that the wheel had "slipped longitudinally" along the pavement; and this holds regardless of whether the wheel axle did move at constant speed, or not.)

How can it be zero when it's in continuous motion?

Well, it bears pointing out what is "in motion" (or at least: of what non-zero speed with respect to the pavement is found), namely: the transient "spot where rubber meets the road"
which on plane ("straight") pavement has the same instantaneous speed wrt. the pavement as has the axle. (Notably, if the pavement is not plane, then the speed of this "spot" may even be arbitrarily large in comparison to $c$, as illustrated for instance by the cycloidal drive. Accordingly one should be careful with attributing "motion" to this "spot"; and its non-zero speed may best be characterized as a kind of phase speed.)

So, an important point to appreciate is that this "transient spot where rubber meets the road" is usually not referred to as "the contact point".