0

I'm trying to figure out a problem involving the motion of a rigid body in 2D. The body has:

  • A translational velocity $\mathbf{v} = (v_x, v_y) $ at its center.
  • An angular velocity $\omega$ around its center.

I am trying to determine the velocity of a point $p$ that is fixed on the rigid body at the local position $(L_x, L_y)$ relative to the body's center.

Given both the translational and rotational components of motion, how do I calculate the total velocity of the point $p$?

Any help with the proper approach or geometric/physical reasoning for how to combine these components would be appreciated!

(It's not the same question as this one. My question is in the context of 2D movement in a plane, not a 1D rolling movement.)

Qmechanic
  • 220,844
Krampfmeister
  • 11

2 Answers2

1

Saying that a rigid body as a whole has translational velocity $\mathbf{v}$ is meaningless.

The right description of the motion of a rigid body requires the velocity $\mathbf{v}_P$ of a material point, $P$, and the angular velocity $\boldsymbol{\omega}$ of the rigid body. Given this two quantities, and the relative position of a material point $Q$ w.r.t. the point $P$, $\mathbf{r}_Q - \mathbf{r}_P$, the velocity of the point $Q$ is

$$\mathbf{v}_Q = \mathbf{v}_P + \boldsymbol{\omega} \times (\mathbf{r}_Q - \mathbf{r}_P) \ .$$

basics
  • 13,368
0

You are asking about the velocity kinematics. The 2D projection of the 3D equation $$\vec{v}_B = \vec{v}_A + \omega \times ( \vec{r}_B - \vec{r}_A )$$ is

$$ \pmatrix{ vx_B \\ vy_B } = \pmatrix{vx_A \\ vy_A} + \begin{bmatrix} 0 & -\omega \\ \omega & 0 \end{bmatrix} \pmatrix{x_B-x_A \\ y_B-y_A} $$

fig1

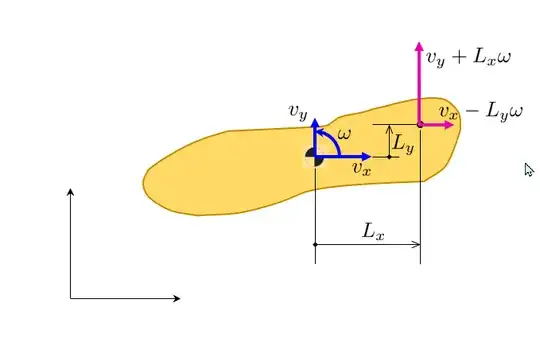
So for your nomenclature and variables the velocity $(vx_P,vy_P)$ at the point P as is relates to the velocity $(vx_C,vy_C)$ at the center of mass is

$$ \pmatrix{ vx_P \\ vy_P } = \pmatrix{ vx_C - L_y \omega \\ vy_C + L_x \omega} $$

The geometric interpretation is take the velocity at the center as it is, and add the rotational component (light blue below) which is perpendicular to the distance vector

fig2

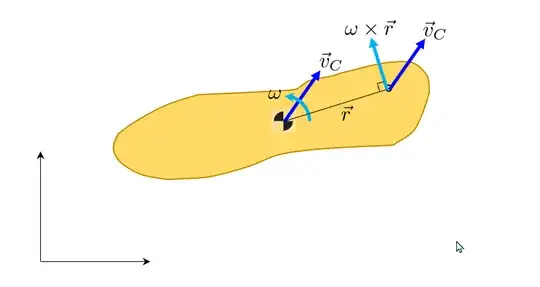
$$\vec{v}_P = \vec{v}_C + \omega \times \vec{r} $$

Of course, the question now is how do you take the cross product of a scalar value like $\omega$.

The answer comes from considering the full 3D vectors and proceed with the cross-product as if the rotation are all out of plane vectors.

$$ \pmatrix{ vx_P \\ vy_P \\ 0} = \pmatrix{ vx_C \\ vy_C \\ 0} + \pmatrix{0 \\ 0 \\ \omega} \times \pmatrix{r_x \\ r_y \\ 0} = \pmatrix{ vx_C - r_y \, \omega \\ vy_C + r_x\, \omega \\ 0} $$

Interestingly, you can find the position $(r_x,r_y)$ that represents the instant center of rotation (which has $\vec{v}_P = 0$) from the equation above

$$ \pmatrix{r_x \\ r_y } = \pmatrix{ \frac{ \mbox{-}vy_C}{\omega} \\ \frac{vx_C}{\omega} }$$

Note that the 3D version of the above is

$$ \vec{r}_{\rm rot} = \frac{ \vec{\omega} \times \vec{v}_C } { \| \vec{\omega} \|^2} $$

John Alexiou
  • 40,139