What actually are virtual particles? In various places around physics SE, documentaries and occasional news headlines, I see the term "virtual particles", normally virtual photons.
I have tried researching it, but I'm not at a level of understanding yet to be able to grasp whats going on, if someone could explain it in a simple manner that would be great.
This is the table of particles on which the standard model of elementary particle physics is founded:
These particles are completely and uniquely characterized by their mass and quantum numbers, like spin, flavour, charge...
The standard model is a mathematical model based on a Lagrangian which contains the interactions of all these particles, and it is framed in the four dimensions of special relativity. This means that the mass of each particle, called rest mass (because it is the invariant mass the particle has in its rest frame) in the energy-momentum frame is given by:
$$m_0^2c^2 = \left(\frac Ec\right)^2 - ||\mathbf p||^2$$ in natural units where $c= 1,$ $$m_0^2 = E^2 -||\mathbf p||^2$$
The standard model Lagrangian allows the calculation of cross-sections and lifetimes for elementary particles and their interactions, using Feynman diagrams which are an iconic representation of complicated integrals:
Only the external lines are measurable and observable in this model, and the incoming and outgoing particles are on the mass shell. The internal lines in the diagrams carry only the quantum numbers of the exchanged named particle, in this example a virtual photon. These "photons" instead of having a mass of zero, as they do when measured/observed have a varying mass imposed by the integral under which they have "existence". The function of the virtual line is to keep the quantum number conservation rules and help as a mnemonic. It does not represent a "particle" that can be measured, but a function necessary for the computation of cross-sections and lifetimes according to the limits of integration entering the problem under study.
p.s. my answer to this other question might be relevant in framing what a particle is.
A virtual particle is a mode in the field that does not obey the dispersion relation for a freely traveling wave. An example of such a relation between angular frequency and the wave vector is: $$c^2\omega^2 = \left(\frac{mc}{\hbar}\right)^2 + \mathbf{k}^2,$$ and the equivalent relationship between energy and momentum. A wave that doesn't obey the dispersion relation is also described as "off mass shell". An example of a field composed entirely of virtual photons is the Coulomb potential produced by a point charge at rest - all of the photons have zero frequency (unchanging), and the density of modes is proportional to $1/\mathbf{k}^2$. That is: $$\frac{q}{4\pi r} = \int -\frac{q}{\mathbf{k}^2} \frac{\operatorname{e}^{i\mathbf{k}\cdot \mathbf{r}}}{\left[2\pi\right]^3}\operatorname{d}^3k.$$ Notice how the virtual photons that make up the Coulomb potential also fail the on shell requirement that the electric field is perpendicular to the wave number - that's because perpendicularity requirement comes from Gauss's law in the absence of charge, and this is a field that only occurs when a charge is present.
In a simpler example, imagine a string fixed at both ends that supports waves with speed $v$. Now imagine pulling the string up at a point, causing it to be two straight lines on either side of the pull instead of one straight line. As long as that string is being held its deflection is composed of virtual phonons because the Fourier decomposition of the string's shape doesn't obey the equations of motion of the free string (that's where dispersion relations come from - the equations of motion). Once the string is let go all of those virtual phonons become "real" when the string starts vibrating. In this example, the external force exerted on the string is like the charge of the particle, so a true particle anti-particle annihilation would require forces acting in opposite directions being rapidly drawn together by the string and releasing waves in the process.
So, you could think of "real" photons as traveling waves that obey Maxwell's equations in the absence of charges. Virtual photons are what you need to describe the field when charges are present.
I can't improve on what is above, but I can illustrate something of a different existential nature. The question "What actually are virtual particles?" is contradictory, for there are no actual virtual particles. Virtual particles are a manifestation of perturbative quantum field theory. The internal lines in Feynman diagrams are propagators with a summation over momentum or energy. As we know from elementary calculus an integration variable is a dummy variable. In many ways the same holds for virtual particles. Virtual particles are a manifestation of our formalism. In many ways they are virtual because they are a mental construction. They are really gadgets we employ to solve problems.
A real particle or just particle is defined as having a mass $m$ that fulfills $m^2 = E^2 -\vec{p}^2$($c=1$) for given $E$, $\vec{p}$. So there is a relation for $E$ and $\vec{p}$ and such particles are called to be on their mass shell(plot $E=\pm \sqrt{m^2+\vec{p}^2}$ for the shell). In contrast, a virtual particle does not fulfill this relation and there is no connection between $E$ and $\vec{p}$ through its mass, it is called to be off its mass-shell.
The concept of virtual particles is an interpretation of intermediate states in scattering processes in quantum field theory that do not obey $m^2 = E^2-\vec{p}^2$. However, there is another interpretation that was used in the early days of quantum field theory and is less used today for symmetry reasons. The idea is to allow the violation of energy conservation for intermediate states in scattering processes. Now, one can fix $m^2=E^2-\vec{p}^2$ and restores that all upcoming particles are real.
So the question for virtual particles is of the same type as the question of how to interpret measurements in quantum mechanics: One has a theoretical concept that gives the right results, but there are no analogues for this concept in our macroscopic world and we therefore are not able to intuitively understand what is going on. Nevertheless, people imagine vivid interpretations about what is truly going on beyond our view. The funny thing is that one can not prove any interpretation to be right or wrong, one can just like or dislike them due to personal favors.
This is a source of much confusion. Before answering what is a virtual particle, one should probably discuss just what is a particle. That is because the word particle doesn't fit particularly well to microscopic nature of matter, quantum fields that are. A macroscopic classical particle has a well-defined position, momentum, and energy at a particular time, but quantum field describing matter necessarily does not.
Think about particle accelerator. There are huge vacuum and particles travelling freely until they interact very briefly at a hot-spot. The incoming and outgoing symptiotically free quantum states propagate conserving momentum and energy for example (these are usually thought as a plane wave solutions and said to be on mass-shell). It makes sense to talk about 245GeV particle for example. Thus, in scattering theory, these incoming and outgoing states are called particles (and perhaps this is where the name particle comes as they resemble classical particles the most when they are free).
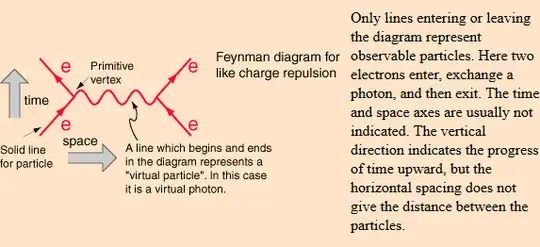
However, during the interaction, it is all a mess. It is not possible to easily identify particles based on their solutions. However, we know exactly how these fields should propagate and that math can be formulated using Feynman diagrams. Two electrons, for example, may exchange a photon. This photon is in the hot-spot and cannot ever be measured. It is inside the Feynman diagram and that is what is normally called a virtual particle.
Now, what I just wrote, is just a definition for particles in the context of scattering theory. There are many others in the context of other theories and they are used to help thinking or at least to name things. The problem is not that there are so many definitions, but the problem is really that the classical particle doesn't suit that well into quantum mechanics.
For example, using strictly this definition, an electron in a hydrogen atom would be classified as virtual as it is constantly exchanging virtual photons with the nuclei and only the photon measuring it should be real. However, in solid-state theory and quantum chemistry, it is very common to speak about that hydrogen 1s electron as a particle. One can also make the ground state of hydrogen vacuum, and speak about holes (electron went from 1s orbital) and electrons (electron at some other orbital). I omitted the prefix quasi here since it is not often used in normal jargon. That is to say, the word electron (or particle for that matter) is very context dependent.
If you ask me, are the virtual particles real and force me to answer with one word, I would say Yes. I would clarify that they are as real as regular particles (in the scattering definition) and our inability to characterize them during interactions doesn't change that. Also, it should be added that the reality of anything is always a metaphysical discussion.
