Significance of wave number?

Question

Till now all I know about the wave number is its formula i.e. ${\frac{2\pi}{\lambda}}$. I always wanted to know what it really means. So can anyone please, explain me its physical significance?

Answer 1

Imagine something oscillating in space and time, for example a plane wave propagating along the axis $x$. This propagation is expressed via the so-called phase $$ \phi(x,t)=\omega \cdot t - k\cdot x = \dfrac{2\pi}{T}\cdot t -\dfrac{2\pi}{\lambda}\cdot x \tag{01} $$ and the magnitude of the plane wave as $$ E(x,t)=A\cos\phi(x,t) \tag{02} $$ As the frequency in time $\:\nu=1/T \:$ gives how many cycles are executed by $E(x_{0},t)$ per unit time $t$ at a specific space point $x_{0}$, so the frequency in space $\:1/\lambda \:$ gives how many cycles are executed by $E(x,t_{0})$ per unit length in space $x$ at a specific time moment $t_{0}$.

EDIT
Both frequencies and consequently the phase (01) are expressed as angles in radian units. A full cycle is a $2\pi $ radians angle. That's why this factor in $\omega=2\pi / T$ and $k=2\pi / \lambda$. \begin{align} T \equiv & \text{time length for a full cycle of the phase at given space point = period} \tag{03a}\\ &\phi(x,t+T) =\phi(x,t)+2\pi \tag{03b}\\ \lambda \equiv & \text{space length for a full cycle of the phase at given time moment = wavelegth} \tag{04a}\\ & \phi(x+\lambda,t) =\phi(x,t)-2\pi \tag{04b} \end{align}

Answer 2

Basically it is whatever you need to multiply a distance by to find a phase difference (in radians).

For a traveling wave, the wave number is the amount of phase difference per unit length.

For a physical sine wave, it is the ratio between the maximal slope of the wave surface and the amplitude. In other words, it measures how dramatic the local differences in displacement can be, relative to the maximal absolute displacement.

Answer 3

The other answers already explain the wave-number as the phase difference per length. Therefore I only elaborate on the 3-dimensional properties of the wave-number.

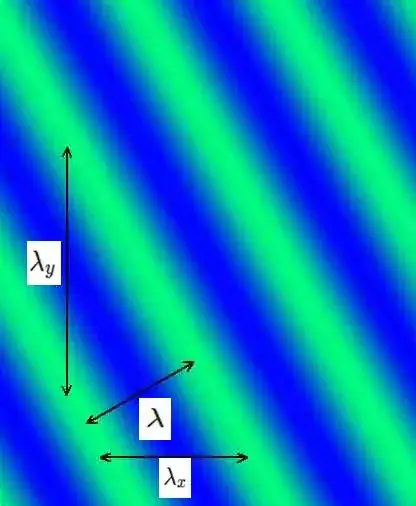
Unlike the wavelength $\lambda$ the wave-number ($k=2\pi/\lambda$) can be regarded as a vector. To understand this consider the image below, showing a plane wave. (I show only in 2 dimensions, because it is easier to draw. But you can do the same reasoning also in 3 dimensions.)

The wave has wavelength $\lambda$. Along the $x$-direction it has a wavelength $\lambda_x$, and likewise, along the $y$-direction a wavelength $\lambda_y$. Notice also that $\lambda_x\ge\lambda$ and $\lambda_y\ge\lambda$.

We see, the Pythagorean relation is not true: $$\lambda^2\ne\lambda_x^2+\lambda_y^2+\lambda_z^2$$

But we have a somewhat similar relation for the reciprocals (see also the Inverse Pythagorean theorem): $$\frac{1}{\lambda^2}=\frac{1}{\lambda_x^2}+\frac{1}{\lambda_y^2}+\frac{1}{\lambda_z^2}$$

It can be shown that the 3 components $(1/\lambda_x,1/\lambda_y,1/\lambda_z)$ have all properties of a vector, including the transformation behavior when rotating the $xyz$ coordinate system.

The wave number vector is defined as $$\vec{k} = \begin{pmatrix} k_x \\ k_y \\ k_z \end{pmatrix} = \begin{pmatrix} 2\pi/\lambda_x \\ 2\pi/\lambda_y \\ 2\pi/\lambda_z \end{pmatrix}$$ Its direction is perpendicular to the wave fronts. This definition includes the factor $2\pi$ ($=360°$) just for convenience, so that $\vec{k}$ gives the phase difference per length, rather than the number of waves per length. Hence the phase difference between two positions separated by $\Delta\vec{r}$ can be calculated by the scalar product $$\Delta\phi=\vec{k}\cdot\Delta\vec{r}.$$