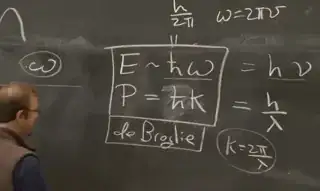Background: I'm currently doing self-study of quantum physics by following university level quantum physics lectures on YouTube (e.g. the YouTube MIT 8.04 Quantum Physics I, Spring 2013 or Stanford Quantum Lectures by Leonhard Susskind, plus supplemental YouTube courses like DrPhysicsA, with the occasional popular level YouTube on specific subjects). My classic math and physics is somewhat robust (high-school) but rusty (about 30 years ago).
In one of the MIT lectures I came about the de Broglie formulas:
I did google and kind of understand how the de Broglie idea for wavelength lambda is determined for a particle with a certain mass (somewhat analog to the Einstein formula for photons) p= h/lambda and then lambda= h/p and then going classic on p via mass*velocity.
However, in the lecture the professor is using $k$ and refers to $k$ as as the wave-number (in conjunction with the reduced Planck constant).
$p = \hbar k $ with
$ k = \frac {2 \pi} \lambda $
So I guess, in intuitive terms (maybe this question is due to my rusty knowledge of classic physics), what's best way to think of $k$? Or maybe someone can just point me to a lecture/explanation of $k$ in terms of classic waves.