Surface tension: the paper clip experiment

Question

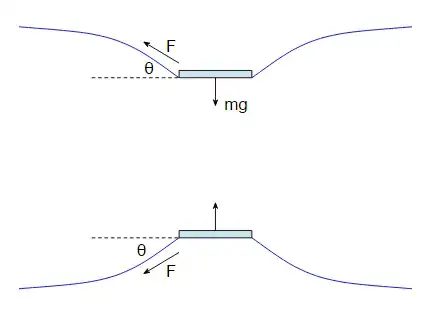
In the paper clip experiment, the surface tension of water prevents the clip from falling, thus we can assume it exerts a force of $mg$ (weight of clip) upwards.

However, if you try to pull the clip out of water, surface tension opposes this motion also. If for simplicity we assume that the clip is a rectangle of length $l$ and breadth $b$, and the surface tension is $T$, then the liquid exerts a downward force of: $$T×2(l+b)$$

What is going on here? Why is there an inconsistency in the direction along which the force acts?

Answer 1

Surface tension always acts in the plane of the surface. The reason it can support a floating paperclip is because the weight of the paperclip deforms the surface downwards:

The surface tension always acts in the plane of the water surface, but because the water surface has been bent downwards to an angle $\theta$ by the weight of the clip there will be an upward component of the force equal $F\sin\theta$. The paperclip floats when this upward force $F\sin\theta$ balances the downward force $mg$ due to the weight of the paperclip.

The second diagram shows what happens as we pull the paperclip upwards. Because the water sticks to the paperclip the result is to deform the surface upwards and this produces a downwards force of $F\sin\theta$.

That's why the force due to the surface tension acts upwards in one case and downwards in the other.