If the Earth was of uniform density then the gravitational acceleration would be greatest at the surface. The graph looks like:
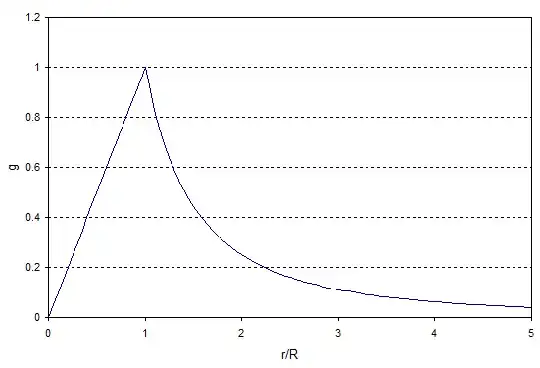
The $x$ axis is radial distance divided by the radius of the Earth, and the $y$ axis acceleration divided by the surface acceleration $g$. However the Earth doesn't have a uniform density because the densest bits (the metallic core) are nearest the centre. The gravitational acceleration actually varies with depth like this:
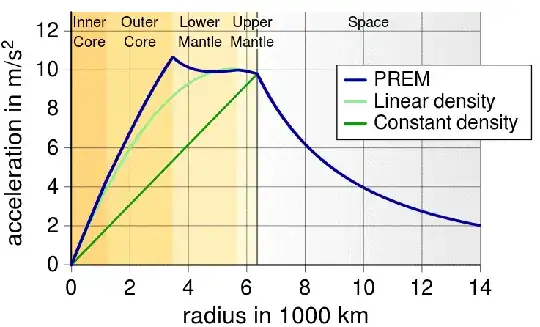
Picture from Wikipedia
So it is, as you say, a maximum at some depth below the surface.
If you were looking at some sort of 3D representation of this it would look like a fuzzily defined spherical shell (actually an oblate shell) and I assume this is what you mean by a doughnut, though note that a doughnut is a distinctly different manifold with a different Euler number and that's why you got criticised for using the term doughnut.
Anyhow, suppose we concentrated more and more of the Earth's mass at its centre, then the maximum acceleration would move towards $r = 0$. The black hole is the limiting case of all the mass being concentrated at the centre, and has the maximum acceleration at the centre i.e. at $r=0$. It does not have a region of zero $g$ at the centre.
I've oversimplified here because you have to be careful what you mean by gravitational acceleration in curved spacetime. A better way to phrase this would be that the relevant Christoffel symbol goes to infinity as $r \rightarrow 0$.

