Particle in a box: value for wave function $u(x)$ when potential $V(x)$ is infinity

Question

The time-independent Schrödinger equation (TISE) is:

$$ -\frac{\hbar^2}{2m}\frac{d^2 u(x)}{dx^2}+V(x)u(x)=Eu(x) \hspace{15pt}$$

where $E$ is a constant.

Imagine now a infinity potential well as we can see on the following picture:

The potential $V$ is infinity in $x<0$ and $x>a$. I've seen on Gasiorowicz's book that $u(x)$ must be 0 for this $x$ interval. But it wasn't totally justified.

I thought about some possibilies but all of them just take me to a place where $u(x)=0$ in $x<0$, $x>a$ is an already assumption . Can you explain me why $u(x)=0$ in $x<0$, $x>a$?

Answer 1

In the $x<0$ and $x>a$ regions the solution will be, respectively, $$u(x)=Ae^{bx} \text{ and } u(x)=Be^{-bx},$$ where $A$ and $B$ are constants to be determined (if necessary) and $b=\frac{\sqrt{2m(V-E)}}{\hbar}$. Next take the limit as $V\to\infty$ with appropriate signs of x in each region.

Answer 2

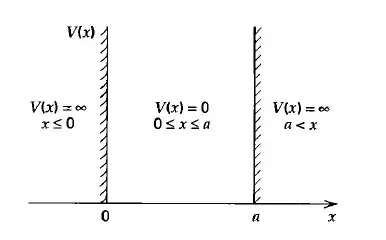
Go back to your time-independent Schrödinger equation: $$ -\frac{\hbar^2}{2m}\frac{d^2 u(x)}{dx^2}+V(x)u(x)=Eu(x) $$ This is a differential equation that must be satisfied for all values of $x$. In particular, if we look at the equation for $x = x_0 > a$, we have $$ -\frac{\hbar^2}{2m}u''(x_0) + (\infty) u(x_0) = E u(x_0) $$ If $u(x_0) \neq 0$, then at least one of two things must be true: $E = \infty$ or $u''(x_0) = \infty$. We presumably do not want the energies of our eigenstates to be infinite, and we presumably want our wave-functions to have well-defined second derivatives (except perhaps at isolated points.)¹ Thus, this is a contradiction, and so we must have $u(0) = 0$ in a region of space where $V(x) = \infty$.

Now, in reality, the infinite potential well should be viewed as the limit of the finite potential well, i.e., take $V = V_0 < \infty$ for $x <0$ and $x>a$ and then take the limit as $V_0 \to \infty$. In such a case, the particle's wave-function would satisfy (for example) $$ u''(x_0) = \frac{2m(V_0-E)}{\hbar^2} u(x_0) $$ which has the solution (for $x < 0$) $$ u(x) = A \exp \left[ \frac{\sqrt{2m(V_0-E)}}{\hbar} x \right]. $$ (There's also a solution with the sign of the square root flipped, but it turns out to be impossible to normalize it.) As $V_0 \to \infty$, we get $u(x) \to 0$ for all $x <0$. Thus, even if we take the limit more carefully, we still get the result that the wavefunction vanishes outside the well as $V_0 \to \infty$.

---

¹ In some circumstances, you can have a function with $u''(x_0) = \infty$ at isolated points; in fact, in this case $u''(0) = u''(a) = \pm \infty$ depending on the eigenstate. But this is only allowable at isolated points, and is really an artifact of choosing a physically unrealistic infinite potential. In reality, potential wells are never infinite, and so the second derivative of the wavefunction is always well-defined everywhere.

Answer 3

Remember that the potential $V(x)$ is related to a force $F(x)$ via:

$$F(x)=-\frac{dV(x)}{dx}.$$

At $x \leq 0$ and $x \geq a$, $V=+\infty$, so in these areas:

$$x \geq a,$$ $$F(x) = -\infty \, .$$

and:

$$x \leq 0,$$ $$F(x) = +\infty.$$

So an infinite force acts on the particle at both borders of these areas, preventing it from entering these areas. In these areas the probability of finding the particle is zero and thus:

$$P(x)=|u(x)|^2=0.$$

and:

$$u(x)=0.$$