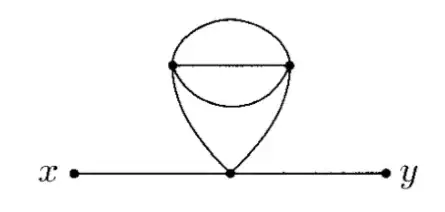
The picture is taken from Chapter 4: 'Interacting Fields and Feynman Diagrams in An Introduction to Quantum Field Theory by Peskin and Schroeder.
There is a two point correlation function $\left<0\lvert\phi(x)\phi(y)\right\lvert 0\rangle$, and the picture is the feynman diagram of one 3rd order term of taylor expansion.
When someone eliminates the coefficient $\frac{1}{3!}$ due to the Taylor expansion, he/she cancels it with the factor due to interchange of vertices (a symmetry factor) with the same value of $3!$.
Also, when someone calculates the symmetry factor, he/she consider the symmetry due to the equivalence of two vertices.
As far as I'm concerned, when you interchange vertices, it involves interchanging the two top "equivalence" vertices of that picture.
So,if "equivalence of two vertices" is not difference from interchanging them, then what's the difference between "equivalence of two vertices" and "interchange of vertices"?