General question about the potential barrier problem: Why does $\exp( kx)$ diverge when $x>0$ in the case when $E < V(x)$?

Question

For the two images below, the first potential barrier has particles approaching it where $E > V_o$ & the second has a particle that has $E < V_o$, where $E$ is the energy of the particles and $V_o$ is the potential of the barrier:

For the first case, when $x < 0$, the particles have a part that is reflected from the barrier (marked by coefficient $B$) and a part that is transmitted (has a coefficient $A$). When $x > 0$, the particles do not have any part that is reflected from the barrier and only a part that is transmitted (has a coefficient $C$).

For the second case where $E < V_o$, the particles again can be reflected or transmitted when $x < 0$, but for the solution when $x > 0$, the book says:

(Images from "Quantum Mechanics Concepts And Applications" by Nouredine Zettili)

My question is:

I am confused about why there is this difference here? What about $E$ being less than $V_o$ that we need to look if $\exp(kx)$ diverges or not? Why was this not taken into account in the first case when $E > Vo$, i.e doesn't $C \times \exp(ikx)$ also diverge in the first case when $E > V_o$?

Answer 1

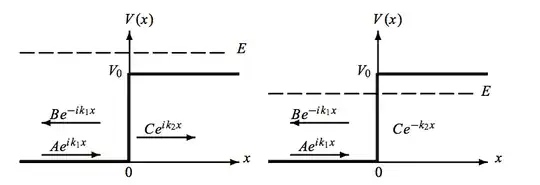
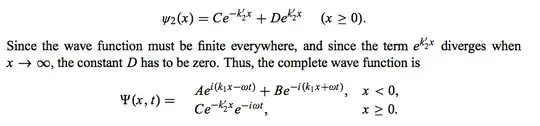For the first case where $E>V_0$ the explanations of user35736 should have clarified things for you. Just bear in mind that solutions of type $e^{ikx}$ in general are trigonometric solutions (oscillatory) and by no means are they exponentially decaying or amplifying, so no problems there. Now I will elaborate on the 2nd case.

First thing you should realise is that $E$ is the total energy of your system. So clearly in the second case when $E<V_0$ the potential is greater than the total energy, such cases we denote as classically forbidden regions, because from a purely classical point of view, the system has 0 chance of being in a state where its potential energy is larger than its total energy or in other words having a negative kinetic energy, unless the system is perturbed somehow of course.

Now in quantum mechanics, the system has a non-zero probability of being transmitted to the classically forbidden regions, in other words the wave function $\psi(x)$ leaks partially into $E<V_0$ region and is partially reflected towards $x<0$ where it undergoes a phase change. But physically we know that the system cannot have a exponentially diverging probability amplitude in the forbidden regions, instead we only look for solution which are rather exponentially decaying, $De^{k'_2x}\rightarrow 0$ and keep the decaying part $Ce^{-k'_2x}.$

From a purely mathematical point of view, wavefunctions that blow up exponentially are not members of our Hilbert space, only those square-integrable ones can be.

Long story short in the case of $E<V_0$ classically one expects the particle to be reflected at $x=0$ and never to get to region $x>0.$ This is not the same in QM, as we find solutions for region $x>0$ as well, $$ \begin{align*} \psi_{\rm x>0} = & Ce^{-k'_2x} \\ k'_2=& \left(\frac{2m|E-V_0|}{\hbar^2}\right)^{1/2} \end{align*} $$

and again the growing exponential part $e^{k'_2x}$ does not belong to the physical Hilbert space and must vanish. But all this means that we nevertheless have a finite probability for finding the particle in the region where its kinetic energy $E-V_0$ is negative. The fact that the particle can penetrate into the classically forbidden regions leads to the phenomenon called tunneling, and the point at which the transition occurs (from one region to another) is called a turning point.

Answer 2

Complex and real exponentials are fundamentally different mathematical objects. Recall Euler's Formula:

$e^{i z} = \cos{z} + i \sin{z}.$

So, for a real value of $k$, we have

$e^{i k x} = \cos{k x} + i \sin{k x}.$

This is a sum of sinusoidal functions - and we know that sinusoidal functions have no limit as $x \rightarrow \infty$ -- certainly they don't go to infinity, since $|e^{i k x}| = 1$ for all $x$.

You can see here a graph of a real exponential (the one that diverges):

http://www.wolframalpha.com/input/?i=e^x+from+x+%3D+-20+to+x+%3D+20

And here you can see the graph of the real and imaginary parts of a complex exponential ($\exp(i k x)$, which does not go to infinity):

http://www.wolframalpha.com/input/?i=e^{ix}+from+x+%3D+-20+to+x+%3D+20

Real exponentials, on the other hand, diverge. We have $\lim\limits_{x \rightarrow \infty} e^{k x} = \infty.$

EDIT: For more info, you may wish to look at this question Boundary Conditions in a Step Potential

Answer 3

Just try to solve the Schroedinger's equation. You'll find that for $x>0$, if you take the solution as $e^{ikx}$, then

$$k=\frac{\sqrt{2m(E-V_0)}}{\hbar}.$$

Now if $E<V_0$, then $k$ is imaginary, i.e. $k_2=ik$ is real, and thus $e^{ikx}=e^{k_2x}$ is real. Thus in case $E<V_0$ one of the solutions vanishes at infinity, and another one diverges due to the properties of exponential function.

Answer 4

I am confused about why there is this difference here? What about $E$ being less than $V_o$ that we need to look if $exp(kx)$ diverges or not? Why was this not taken into account in the first case when $E>V_o$, i.e doesn't $C×exp(ikx)$ also diverge in the first case when $E>V_o$?

The other answers have explored the question of why there are different forms of the solution for $E>V_o$ versus $E<V_o$. @user35736 also noted that the forms for $E>V_o$ are trigonometric and will not diverge as $x\rightarrow \pm\infty$.

So let's take a 2nd look at the $E<v_o$ situation. The general solution in that region will be $$\psi(x\ge0)= Ce^{-k_2'x}+De^{k_2'x}$$. As noted in the OP statement, we need to investigate this as $x\rightarrow\infty$ because we insist (as other answers note) that valid, normalizable wave functions must be bounded. The $Ce^{-k_2'x}$ is bounded but the $De^{k_2'x}$ isn't (and here's the additional point) because the potential $V_o$ remains larger than E for all x>0. If at some finite value $x_2>0$ the potential becomes less than E, then we must keep the $De^{k_2'x}$ term and connect it to a third regional contribution to $\Psi(x,t).$ And to first-order, ignoring this term is a good approximation if the possible $x_2$ is much larger than $1/k_2'$.

Answer 5

Usually one requires, that the propability density $\varrho = |\Psi(x)|^2$ is integrable over the whole range (suchs that it can be normalzied). In this sense $\Psi(x) = \exp(kx)$ is just as divergent as $\Psi(x) = \exp(ikx)$, since the limit $$\lim_{\epsilon \rightarrow \infty } \int_{-\epsilon}^\epsilon |\Psi(x)|^2 \ dx$$ does not exists in both cases.

But there is still a difference. Assume we are interested in statements like "this is double as propable than that". One does not need a normalzied propability density for these situations, since by comparision the normalization constant will cancel. One can think of another condidtion for these situations. E.g. the integral that gives us a mean value $\bar{\varrho}$ for $|\Psi(x)|^2$ on some range $R = [-\epsilon,\epsilon]$ $$ \bar{\varrho} = \frac{1}{2\epsilon} \int_{-\epsilon}^{\epsilon} |\Psi(x)|^2 \ dx $$ should be convergent for $\epsilon \rightarrow \infty$. This is a weaker condidtion that incorporates the usuall normalization condidtion.

Now the point is, this condidtion does hold for $\Psi(x) = \exp(ikx)$ but not for $\Psi(x) = \exp(kx)$ showing that the propability density is not bounded for the later case.