There is an account on dualities in quantum field theories and string theories by Polchinski from last week
http://arxiv.org/abs/1412.5704
At the end of page 4, he writes the wave/particle dichotomy arises from different limits you can take in a quantum field theory.
Which limits are meant here exactly, and can one give a proper example? I assume it might relate to many/few quanta states.
There are probably various answers to this question and I will try to provide one that I consider quite interesting. It is a specific realization/example of the fact that the path integral is dominated by estrema of the action.
The wave aspect of a QFT is probably trivial as QFT is dealing with wave equations. This is particularly apparent for massless particles and I will not discuss it any further.
Let me thus focus instead on the opposite limit when the particles are very heavy. I will use the Schwinger proper time and heavily follow Matt Schwartz textbook.
For simplicity, consider the propagator of a scalar particle in an external field source $A_\mu$ that in the Schwinger proper time takes a path-integral form over the particle trajectory $$ G_A(x,y)=\langle A|T\phi(x)\phi(y)|A\rangle=\int_0^\infty ds e^{-is m^2}\langle y| e^{-i\hat{H}s}|x\rangle $$ where $$ \langle y| e^{-i\hat{H}s}|x\rangle =\int_{z(0)=x}^{z(s)=y} [dz(\tau)] e^{i\mathcal{L}(z,\dot{z})} $$ with $$ \mathcal{L}=-\int_0^s d\tau \left(\frac{dz^\mu(\tau)}{2d\tau}\right)^2+e \int A_\mu(z) dz^\mu\,. $$ It is convenient to rescale the variables with the mass, $s\rightarrow s/m^2$ and $\tau\rightarrow/m^2$ so that the path-integral is clearly dominated by the free kinetic energy when the mass is large $$ G_A(x,y)=\frac{1}{m^2}\int_0^\infty ds e^{-is}\int_{z(0)=x}^{z(s/m^2)=x} [dz(\tau)]e^{-i\int_0^s d\tau m^2(\frac{dz^\mu}{d\tau})^2+i\int eA_\mu dz^\mu} $$ This is the limit of particle that takes a well definite trajectory since the path-integral is dominated by the point of stationary phase that corresponds to the free particle solution $$ z^\mu(\tau)=x^\mu+\tau v^\mu\qquad v^\mu=(y-x)^\mu/s\,. $$ Moreover, on this solution the propagator becomes (after rescaling back to the original variables) $$ G_A(x,y)=\int_0^\infty ds e^{-i\left[s m^2+\frac{(y-x)^2}{4s}-ev^\mu\int_0^s d\tau A_\mu z(\tau)\right]} $$ where the last term is the same that one get by adding the source current $$ J_\mu=v_\mu \delta(x-v\tau) $$ so that the heavy particle creates the field $A_\mu$ as if moving in a classical trajectory at constant speed. As Schwartz says, when a particle is heavy the QFT can be approximated by treating the particle as a classical source (but treating everything else as quantum, e.g. the particle can possibly generates quantum radiation $A_\mu$ upon which we haven't integrated over yet).
These might be two different issues. Wave-particle duality is one issue, different classical limits is another issue.
Wave-particle duality often refers to the fact that when choosing an experiment historically, people sometimes chose options that revealed wave properties and sometimes chose options that revealed particle properties. So the hypothesis was that nature has both qualities waiting to be revealed by different choices of experimental setups that measure the same initial input.
As for classical limits, (assuming you aren't doing MIW or dBB) a classical limit is one where you can ignore (relative) phases (classical fields and particles are entirely real, they have no phase).
For a bosonic field, you can take something like a classical wave limit. You have the option to take a high quantum number limit that is also a coherent state, then there is no relative phase, so the phase can be ignored, and it looks like a classical field. So it's not just a high quanta limit, you also need the coherence. I didn't go into much detail because Motl seems to cover it in detail at the level you are looking for in http://motls.blogspot.com/2011/11/how-classical-fields-particles-emerge.html
You can also take something like a classical particle limit, this is a low quanta limit but also a limit where the energy is kept high. So for the electromagnetic case, this would be single gamma rays, and now the scattering of a single quanta (where QFT reduces to just relativistic quantum mechanics since there is only a single quanta). In this limit the phase doesn't matter for the scattering angle, and you can compute it as compton scattering by a photon of fixed momentum $h\nu$. The details about the QFT to RQM limit (single quanta) is well known and how the high energy RQM scattering reduces to that of compton scattering I think is simply because there are so few options that conserve energy and momentum and scattering states have to be on shell. Again, probably well known.
None of this is as deep as I think you expected, but I wanted to provide the filling in of what I thought the authors meant and it might be things you probably already knew but they just didn't give enough details for you to know it was stuff you already knew.
Wave particle duality is not a quantum physical issue! Here is a full description of its simple mechanism, exclusively based on special relativity which is easily understandable by any interested person.
Wave-particle duality is deeply embedded into the foundations of quantum mechanics (Wikipedia).
This statement is entirely disproved in the following by showing one case which may entirely be explained classically: light in vacuum.
The following derivation is based exclusively on the two postulates of special relativity from which is resulting directly and compellingly the entire model for light in vacuum.
There is one unexplored zone in special relativity which seems to yield only meaningless results. When particles are moving not only near speed of light (v < c) but at speed of light (v=c), the Lorentz transforms cease to operate. The proper time is reduced mathematically to zero, but there is no reference system from which this could be observed. Also, lengths would be reduced to zero for such a hypothetical non-existent reference system.
As a consequence, up to now the corresponding equations deriving from special relativity (time dilation and length contraction) were simply confined to massive particles, excluding the case v=c from the domain of definition of these equations. There is no physical legitimation for such a break in their application (implying de facto a limitation of universal validity of special relativity), and Einstein's special relativity does not cease to exist at v=c as it is shown by the means of an example in the following chart:
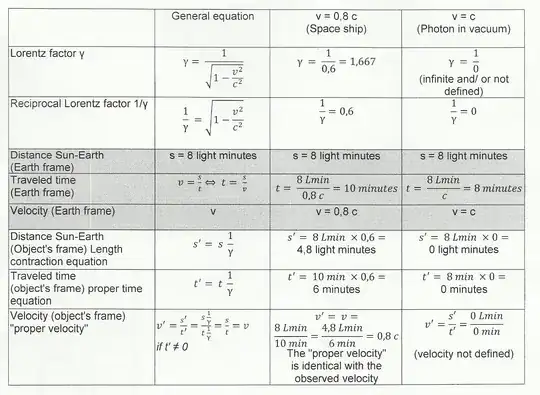
By consequence, it follows from the equations for proper time and length contraction that a photon which is traveling the distance Sun-Earth according to our observations in t=8 minutes for a distance of s=8 light minutes, has from its (hypothetical) own point of view a proper time t'=0 and travels a distance s'= 0.
If time and traveled distance are both zero that would mean that there was no movement. When I am traveling zero meters in zero seconds, I did not move, and there is no movement which could be subject to a measurement of velocity. My velocity is not defined (0m/ 0 sec.)
The Lorentz factor splits realities
The twin paradox shows with unequaled clarity the effects of the Lorentz factor.
Example: A twin brother undertakes a space travel and returns after 20 years. At his return to Earth the twin brother who remained at home observes that the traveling twin aged only by 5 years.
In this example the observed time on the observer's clock is 20 years. The proper time (and thus the real aging) is only 5 years instead of 20 years. These two realities are linked arithmetically by the proper time equation and by the Lorentz factor.
Moreover we can notice a hierarchical order of realities: We cannot say that the traveling twin has become 20 years older, even if all observers on Earth have measured 20 years. This would be in contradiction with the physical condition of the traveling twin who looks younger than the twin who stayed on Earth. This means with regard to photons that the proper reality of the photon, even if it may not be observed by anyone, reflects its primary reality. All observations are secondary with regard to this primary reality. Even the constant of speed of light c.
By consequence, and in accordance with the wording of the second postulate of special relativity, light velocity c is a secondary observer's reality. We observe a movement of light which according to the primary reality of the photon is a standstill.
The Lorentz factor is assigning to photons two realities, that means, the transmission of the light momentum is double-tracked:
The secondary reality is the (commonly known) observed reality: Maxwell equations are describing a light quantum in the form of an electromagnetic wave moving at speed of light (v = c, t = 8 min, s = 8 light minutes). The transmission of the momentum occurs indirectly from Sun to the wave and then from the wave to Earth.
The primary reality is the unobserved proper reality of the photon: t'=0 and s'=0, proper time and distance are zero, there is no velocity. That means that the momentum is transmitted directly outside of spacetime from Sun to Earth, without intermediate medium.
Result:
A classical explanation of Young's double slit: while we are observing nothing but an interfering wave, the particle characteristics of light in vacuum are transmitted directly (path length = 0) and in parallel to the electromagnetic wave.
Light in vacuum is a primitive border case of quantum physics which can be explained classically. As a result, the mere wave-particle duality can be described without non-locality issue (see also the open (former bounty) question) as a classical phenomenon.
This fact does not change at all quantum physics with all its non locality issues. But it shows that there is one classical case of wave-particle duality, with no need of recourse to quantum mechanics and/ or QFT.
A simple answer to the question of NikolajK and John Rennie what the nature of wave-particle duality is.
