Help understanding Bell's spaceship paradox

Question

The problem statement of Bell's Spaceship paradox is this:

Two spaceships float in space and are at rest relative to each other. They are connected by a string. The string is strong, but it cannot withstand an arbitrary amount of stretching. At a given instant, the spaceships simultaneously (with respect to their initial inertial frame) start accelerating (along the direction of the line between them) with the same acceleration. (Assume they bought identical engines from the same store, and they put them on the same setting.) Will the string eventually break?

And the solution is here: http://www.physics.harvard.edu/uploads/files/undergrad/probweek/sol11.pdf

The very first statement made in the solution to this problem is "To an observer in the original rest frame, the spaceships stay the same distance, d, apart.". But why do they stay the same distance apart to an observer in the original rest frame? Shouldn't the distance between the spaceships undergo length contraction, as they are connected by a rope? I asked a similar question here, and the answer that I got was that

Length contraction only applies to situations where you have a system with two "ends" that are moving at the same velocity, and you know the distance L between these ends in the frame S where they are at rest, and want to know the distance L' between them at any given instant in some other frame S' where they are moving at velocity v along the axis joining the two ends.

Well the two ends of the rope are moving at the same velocity, I know the distance between them at frame $S$ when they are at rest, and I do want to know the distance between them at any given instant when they are moving at velocity $v$ along the axis joining the two ends. How then can I make the statement that for an observer in the rest frame that the spaceships stay the same distance, $d$, apart?

Answer 1

Bell's thought experiment is set up in such a way that the distance between the ships, call it $d$, remains the same in the stationary frame; after all, both ships have the same velocity $v$ at the same time $t$, so their distance never changes. Let's use $(x,t)$ as coordinates in the stationary frame and $(x',t')$ in the space ships' frame, we have $\Delta x = d$ if the positions are measured simultaneously, i.e. $\Delta t = 0$. Applying the Lorentz transform, we find $$ \begin{align} \Delta x' &= \gamma\left(\Delta x - v\Delta t\right) = \gamma d,\\ \Delta t' &= \gamma\left(\Delta t - \frac{v}{c^2}\Delta x\right) = -\gamma\frac{vd}{c^2}. \end{align} $$ So the distance between the ships in the moving frame does increase: $d'=\gamma d$. Notice also that there is a simultaneity issue: in the moving frame, the space ships are at rest at different times. You can argue that this complicates the notion of a distance in the moving frame. However, we can solve this if we switch off the accelerations simultaneously in the stationary frame; then both ships will have the same constant $v$, and both ships will stay at rest in the moving frame, so it doesn't matter at which time their position is measured: their distance will be $d'=\gamma d$, so the rope between them will break.

Note that there's no real paradox here: the distance $d'$ between the ships, measured in their rest frame, is Lorentz-contracted to $d$ when the ships are observed to be moving with respect to a stationary frame. It only seems odd because this thought experiment is set up in such a way that $d$ doesn't change; whereas in the usual discussion of length contraction one defines $d'$ as the constant length. It's simply a matter of different conditions.

Now, one can ask if it's possible to accelerate the space ships in such a way that the rope doesn't break. The answer is yes: it's called Born rigid motion. A discussion is given in this paper, which I will summarize here. I first need to introduce the concept of proper acceleration. Unlike normal coordinate acceleration, proper acceleration is Lorentz invariant: see this post and this post for more information. In the absence of perpendicular velocities, the proper acceleration $\alpha$ is given by $$ \alpha = \gamma^3\frac{\text{d}v}{\text{d}t} = \frac{1}{(1 - v^2/c^2)^{3/2}}\frac{\text{d}v}{\text{d}t}.\tag{1} $$ Now, let's call the first space ship $A$ and the second $B$, and we each give them a different but constant proper acceleration, $\alpha_A$ and $\alpha_B$. Since the ships have different accelerations, they will have the same velocity $v$ at different times $t_A$ and $t_B$. It's straightforward to derive the velocity of the ships from (1) as $$ \begin{align} v &= \frac{\alpha_A t_A}{\sqrt{1 + \alpha_A^2 t_A^2/c^2}} = \frac{\alpha_A t_A}{\gamma},\\ v &= \frac{\alpha_B t_B}{\sqrt{1 + \alpha_B^2 t_B^2/c^2}} = \frac{\alpha_B t_B}{\gamma}, \end{align} $$ where we used the property $$ \gamma = (1-v^2/c^2)^{-1/2} = \sqrt{1 + \alpha_A^2 t_A^2/c^2} = \sqrt{1 + \alpha_B^2 t_B^2/c^2}. $$ Their positions, initially a distance $d$ apart, are then $$ \begin{align} x_A &= \frac{c^2}{\alpha_A}\left(\sqrt{1 + \alpha_A^2 t_A^2/c^2} - 1\right) +d = \frac{c^2}{\alpha_A}(\gamma -1) +d,\\ x_B &= \frac{c^2}{\alpha_B}\left(\sqrt{1 + \alpha_B^2 t_B^2/c^2} - 1\right) = \frac{c^2}{\alpha_B}(\gamma -1). \end{align} $$ If we use the shorthand notation $$ \delta = \frac{c^2}{\alpha_A} - \frac{c^2}{\alpha_B}, $$ we find, $$ \begin{align} \Delta x &= x_A - x_B = (\gamma - 1)\delta + d,\\ \Delta t &= t_A - t_B = \frac{\gamma v}{c^2}\delta. \end{align} $$ The corresponding distance in the moving frame is $$ \Delta x' = \gamma\left(\Delta x - v\Delta t\right) = \delta - \gamma\delta + \gamma d. $$ Now, we impose the condition $\Delta x' = d$, such that the rope doesn't break. This implies a relation between the accelerations $$ (1-\gamma)\delta = (1-\gamma)d, $$ in other words, $$ \delta = \frac{c^2}{\alpha_A} - \frac{c^2}{\alpha_B} = d. $$ Therefore, the second space ship has to accelerate more than the first, and their distance will appear shortened in the stationary frame (if measured at the same time $t$). We also see that $$ \Delta t' = \gamma\left(\Delta t - \frac{v}{c^2}\Delta x\right) = \gamma\left( \frac{\gamma v}{c^2}d - \frac{v}{c^2}(\gamma - 1)d - \frac{v}{c^2}d \right) = 0. $$

Answer 2

"To an observer in the original rest frame, the spaceships stay the same distance, d, apart.". But why do they stay the same distance apart to an observer in the original rest frame?

The spaceships move with constant mutual distance in the original rest frame, since their corresponding parts have the same velocity function of time. The description of the situation in the original question directly implies this.

Shouldn't the distance between the spaceships undergo length contraction, as they are connected by a rope?

No, this would be contrary to the specified situation.

Answer 3

I've read your question a number of times in order to try and understand precisely what is puzzling you about this well known 'paradox'. It seems to me that this is it:

Well the two ends of the rope are moving at the same velocity,

Let's stipulate that, in the inertial frame of reference in which the two spacecraft are initially at rest, the two ends of the rope have the same instantaneous velocity. Then, it follows that the length of the rope, as measured in this frame, is constant and equal to the length of the rope when the rope was initially at rest: $L = L_0$.

This must be the case since the world lines of the ends of the rope are, by stipulation, congruent.

Now, imagine another inertial reference frame with relative speed $v$ in which the rope is momentarily at rest* and that, in this moment, the rope is measured to have length $L'$.

According to the Lorentz transformations, it must be the case that

$$L' = \gamma_vL > L_0$$

In other words, in a momentarily co-moving reference frame, the measured rope length must be longer than the rope's initial rest length.

Let's summarize:

1. We stipulate that the ends of the rope have the same velocity in the initial rest reference frame
2. Thus, the length of the rope in the initial rest reference frame is constant and equal to the initial rest length of the rope
3. Thus, the length of the rope in a momentarily co-moving reference frame is longer than the initial rest length of the rope

So, to answer this question:

Shouldn't the distance between the spaceships undergo length contraction, as they are connected by a rope?

As I've shown above, if we stipulate that the ends of the rope have the same velocity in the initial rest frame, it follows that the length of the rope (and therefore the distance between the spaceships) must be greater in a momentarily co-moving reference frame than the initial rest length of the rope.

---

*In fact, this is not quite possible. Only in the initial rest frame do the two ends of the rope have the same velocity. In a relatively moving inertial frame, the ends of the rope have different velocities so the statement "the rope is momentarily at rest" isn't well defined. This is a subtle point that is discussed more completely here.

Answer 4

I think that the fact that the clocks in the two ships appear synchronized to the initial observer in S distracts us and makes us think of the situation in non-relativistic terms. In general, most SR paradoxes can be eased by remembering the relativity of simultaneity. Let's say that the 2 spaceships have clocks at their centers, and the observer in S finds them to be synchronized throughout. What jolts us back into an SR view of the situation might be to point out that for that observer in S, a clock in the back of each ship appears to be set later than the clock in the front of that same ship. The "sameness" of the clocks in the two ships now appears much more artificial and "set up."

Answer 5

I had to go back to this paradox again because something came up that proved to be even more critical in it's resolution. Forget the explanation thus far given - there is no paradox here - because there is no experiment - the scenario for the experiment makes one very flawed assumption - that is there are three separate systems, when in fact there's only one. The two spacecraft will of course be able to adjust their rocket motors in such a way that the string will be kept taught at all times - this very action in itself transfer's energy & weight throughout the system in such a way, it would be as if there was only one spacecraft being accelerated & the string would be a intrinsic part of that spacecraft. I have dealt with the "Bells Spaceship Paradox" many times over the years & have only just for the first time come across this not so obvious flaw in this ingenious "Thought Experiment". I really should have picked up on this years ago - I could kick myself - but never mind - I'm not the first - & I certainly will not be the last. It's often the case with paradoxes - it's not so much resolving them as realizing there is no paradox to begin with. The first spacecraft is effectively tugging along the second spacecraft, but the second spacecraft is imparting just enough power to it's motors to allow the spacecraft to be hauled without the string snapping i.e. the string is relieved of the required amount of stress & strain, such that the critical elastic limit is not exceeded. This then is one system - it is not three. You could get all pedantic - but then you'd have to invoke the "Heisenberg Uncertainty Principle" - I don't think there's a physicist around in their right minds would argue with him !

Answer 6

Ok, lets' say that at a distance from the earth, 3 spaceships were constructed. There were two small ships, and one long mother ship. Each ship was programmed to accelerate in the same manner, such that a specific G-force curve is followed as motion begins, and this is continued onward up until the intended target velocity is achieved.

Each ship is sent to mars, as a test run. Each ship takes exactly the same amount of time to reach mars, right down to the second.

The ships were then returned to Earth and were relatively positioned, as shown in the above diagram. The mother ship has two bubble windows, and each small ship has one bubble window. People inside the A and B ships can look across at others located in the mother ship, and do so via looking out the bubble windows.

Once again all 3 ships head off to mars, but now they do so with all 3 departing at the very same moment.

Moving together, they all share a common frame. As they move faster and faster toward mars, everything seems to be the same to the observers that are located within space ships A and B. To each of them, they are still looking directly on over toward the mother ship bubble that is located immediately across from them, all this occurring right up to and including reaching the intended target velocity.

However, this time the space ships will not stop at mars, but will pass by mars.

All due to the velocity of the mother ship, to the observers on mars, the ship now appears to be half length in comparison to its originally designed length. This also applies to ships A and B. Also noted is the fact that spaceship A's bubble is still in line with the mother ships rear bubble, and space ship B's bubble is still in line with the mother ships front bubble. With this being the case, the observed spatial distance between spaceship A and B, has reduced to half its previous distance as well. Therefore, logic says that the string which is connecting A to B, would not have broken.

Answer 7

A while back, I generated illustrations for a treatment of this problem in The Physics FAQ. You can read my updated illustrated version in full on my mirror here. Here is a paraphrased conclusion:

---

How did the ships get farther apart, if they maintained the same constant acceleration at all times?

As shown in the following drawing, for any chosen P except for right at the starting gate, the xʹ axis will always be tilted up a little, and not parallel with the x axis.

   

Physically, this means that while the left-hand ship is instantaneously at rest in the coordinate system drawn around P, the right-hand ship is not at rest. In the ship’s reference frame, the second ship is always moving faster!

In [these illustrations], you can see that the paradox is resolved due to failure of simultaneity. The two ships have the same velocity at the same time in the lab-frame, but the “same time” is different in the co-moving frame. The trailing ship sees the lead ship farther ahead in time, and during that extra time it will have moved farther ahead and gained more speed.

   

The red dots are the ships P and Q at the same time (violet line) according to the guy who arrived too late to take the flight and is still waiting on standby at the port. The blue line is second ship's space axis through its instantaneous velocity at Q. The green hyperbola shows its actual world line since it is accelerating.

In the above detail, both ships have the same time, according to their on-board clocks, at points P and Q respectively. However, when the observer on the first ship reaches point P, he determines that the second ship, at that very moment, is well ahead of Q. In particular, it is where the xʹ axis (brown line) intersects the green curve. Every event along the xʹ line is at the same time as P, differing only in position, in P’s reference frame.

The faster the trailing ship goes, the greater the lead ship’s head start! Spacetime rotates around the poor pursuer dooming him to give his opponent a greater advantage as he increases his own velocity. In Special Relativity, acceleration is a rotation of the 4-dimensional velocity vector in spacetime.

Answer 8

Joshua, there is no paradox here.

For a start, notice that the paradox is based on contradictory assumptions. In the link you provide it says:

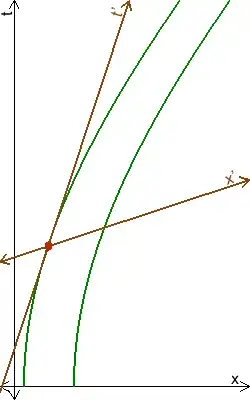
The distance between the spaceships does not undergo Lorentz contraction with respect to the distance at the start, because in S it is effectively defined to remain the same, due to the equal and simultaneous acceleration of both spaceships in S.

If the acceleration of both spaceships is equal and simultaneous in the frame in which they are moving (and providing we are allowed to use SR for accelerated movement), than at any (period of) time any pair of points located in this frame of reference must undergo exactly the same movement, and therefore the same change of distance between them as demanded bu Lorentz Transforms. See my answer on SE where the concept of space contraction in SR is illustrated.

So if both ends of Spaceship A undergo the same acceleration $a$, and if both ends of Spaceship B undergo the same acceleration $a$, than also the points at both ends of the rope (denoting the distance between the ships) undergo the same acceleration $a$. Therefore, if Spaceship A is contracted, and Spaceship B is contracted, then also the distance between them must be contracted. So if accelerations are equal and simultaneous than the distance between the ships cannot remain constant. (despite what the experiment assumes)

On the other hand, if the distance between the spaceships is to remain constant, than the accelerations of the spaceships must not be equal and simultaneous in the frame in which they are moving, if one wants to claim SR holds true for this movement. (again, despite what the experiment assumes)

One cannot postulate that all the points in a frame undergo the same movement at any given time, and yet distances between them change contrary to the conditions set for this movement.

---

Also, the entry Special Relativity in Wikipedia still reads:

In physics, special relativity (SR, also known as the special theory of relativity or STR) is the accepted physical theory regarding the relationship between space and time. It is based on two postulates: (1) that the laws of physics are invariant (i.e., identical) in all inertial systems (non-accelerating frames of reference); and (2) ...

So, despite what you might find in the very formulation of this paradox, as well as in other answers and comments to your question, the postulate of non-accelerated relative motion in SR is still upheld by mainstream physics. And this site is supposed to stick to mainstream physics.

---

Should you be curious, however, how the acceleration was introduced to SR: Well it was sneaked in illegally through a non-physical trick:

• The proponents say there exist "momentarily co-moving" inertial frames of reference (see Alfred Centauri's answer), which means that time is supposed to stop "momentarily" which makes the accelerated motion non-accelerated. Well, these mathematicians forget that in physics once you stop time, you also stop all motion (movement is defined as a change in position, and you cannot change position in no time, because this would imply infinite velocity, which is forbidden by the very SR), which means you cannot apply any transforms to the situation at all. Tricks are for kids ...

• Additional proof that above is cheating in order SR to illegally sneak in acceleration. I followed the link Alfred Centauri provided in his answer, and there we have: "Also, d˛x/dt˛ = 1 at t = 0. [Translation: Initial acceleration is 1.]." So no time has passed (Δt=0) and yet a ship acquired a non-zero acceleration?! But in his answer wrote: "...imagine another inertial reference frame with relative speed v in which the rope is momentarily at rest". "Momentarily" means Δt=0 again, and yet this time we have inertial frame. And this "momentarily inertial frame" was necessary to claim that accelerations are allowed in SR.

So when they need acceleration, they can have it at Δt=0, but when they need an inertial frame they get it from the same Δt=0 as well? Now, are we still talking physics here?

---

John Rennie here on SE also contradicts it. He says that the very space is contracted at relativistic speeds. In the answer to the question: "How long would it take me to travel to a distant star?", he said: "If the spaceship is travelling at velocity v relative to the Earth and destination star then the Earth and star are travelling at velocity v relative to the spaceship, and the crew of the spaceship see distances contracted by the Lorentz factor". If distances are contracted then Bell's spaceships do not retain the same distance d as seen by stationary observer.

You can use a more straightforward logic, though.

Lorentz Transforms show distance contraction between any two points moving at relativistic speed. The equation does not care if the points belong to a single body or two. If you wield the spaceships together using a metal rod, you can claim this is just one spaceship (always measured to move at $v$ throughout the whole length: SpaceshipA+String+SpaceshipB). By the same logic you could say the spaceships should break, because there is space inside them which does not undergo contraction, and so the chassis of the spaceship will be stretched. Should someone say the space is within the spaceship, and so it moves, I will ask, what if the design of the spaceship demands there are areas of outer space allowed within the spaceship construction? Will the chassis brake then?

And the last - and final - blow. Due to the very axioms of SR the spaceships connected by a rope can always be treated as stationary, and everything else moving at relativistic speeds. Therefore, the spaceships do not even have to accelerate to be seen as moving at relativistic speed from some other frame (itself accelerated to relativistic speed). So, should we assume the string will brake only because someone claims he sees the distance $d$ between the ships unchanged? Absurd!

(In his comment below Ján Lalinský said that we are dealing with accelerations here, which disproves my argument above. Well, SR is based on the axiom that there are no preferred frames of reference. Assuming that acceleration forbids me from treating the spaceships' frame of reference as stationary means also that preferred frames do exist in SR. Which is contrary to the axioms of the very theory we are basing our reasoning here.

Still, even if accelerations were admitted in SR, one would have to prove that in such case distance between moving points should change differently than it does in its classical version - without accelerations - and not contract.)

The logic of SR demands that the distance between any two relativistically moving points be contracted. Therefore this is a manufactured paradox. Shame it is still upheld by Wikipedia and top universities.