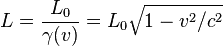A simple proof for time dilation can be found here
What I am confused about is that when the proof calculates the longer distance light has to travel, doesn't it ignore the effects of length contraction, which will occur at relativistic speeds?
According to the diagram shown, the horizontal component if you will of the distance traveled is simply the velocity times the time, but I thought that the length would be contracted as I am a moving observer?
Is there a flaw in my logic?
Length contraction only applies to situations where you have a system with two "ends" that are moving at the same velocity, and you know the distance L between these ends in the frame S where they are at rest, and want to know the distance L' between them at any given instant in some other frame S' where they are moving at velocity v along the axis joining the two ends. That "at any given instant" is key--you must be talking about two events on the worldlines of the ends that are simultaneous in frame S'. If on the other hand you have two events that are not simultaneous in either of the frames you're considering, like the event of a light ray leaving the bottom mirror and the event of the light ray arriving at the top mirror, then you can't use the length contraction equation to relate the distance between the events in frame S to the distance between them in frame S'. Instead, if S' is moving at speed v in the +x direction relative to S, you can use the full Lorentz transformation equations on the position and time intervals $\Delta x$ and $\Delta t$ between the pair of events:
$ \Delta x' = \frac{1}{\sqrt{1-v^2/c^2}} (\Delta x - v\Delta t)$
$ \Delta y' = \Delta y $
$ \Delta z' = \Delta z $
$ \Delta t' = \frac{1}{\sqrt{1-v^2/c^2}} (\Delta t - v\Delta x/c^2)$
And the reverse version:
$ \Delta x = \frac{1}{\sqrt{1-v^2/c^2}} (\Delta x' + v\Delta t')$
$ \Delta y = \Delta y' $
$ \Delta z = \Delta z' $
$ \Delta t = \frac{1}{\sqrt{1-v^2/c^2}} (\Delta t' + v\Delta x'/c^2)$
Note that the first of the reverse equations reduces to the length contraction equation in the specific case where $\Delta t' = 0$ (the two events are simultaneous in S') and $\Delta x' = L'$--in that case $\Delta x = L = \frac{1}{\sqrt{1-v^2/c^2}} (L' + v*0)$, so $L' = \sqrt{1 - v^2/c^2} L$. But you aren't allowed to use the length contraction equation in other situations.
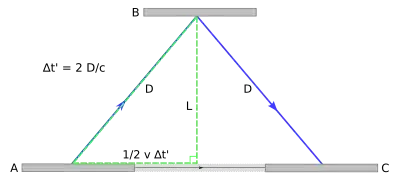
You could imagine we had a rigid measuring-rod that stretched vertically from one mirror to the other, of course--then it does have two "ends", and you can ask about the distance between them at any given moment in the frame where the light-clock is moving horizontally. But as I said in my first sentence, the length contraction equation only applies when you're using a frame where the ends "are moving at velocity v along the axis joining the two ends"--in this example, the axis of motion is horizontal, whereas the axis joining the two ends is vertical. You can see from the Lorentz transformation equation that even if $\Delta t'=0$ for two events, if their separation is entirely along the y and/or z axis, so they have zero spatial separation $\Delta x'$ along the axis that the two frames are moving relative to one another, the distance between these events will be the same in both frames since $\Delta y = \Delta y'$ and $\Delta z = \Delta z'$. Sometimes this is stated succinctly by noting that "length contraction is only along the axis of motion".
Finally, note that every frame defines the "speed" of anything in that frame as the rate that the position coordinate is changing with the time coordinate, using the coordinates of that frame. So if you have two events on the worldline of a particle moving at constant speed, and you know the position and time coordinate intervals between the events in some frame, by the Pythagorean theorem the total distance between the two events will be $\sqrt{\Delta x^2 + \Delta y^2 + \Delta z^2}$ in this frame, so by definition the speed of the particle in this frame must have been $\frac{\sqrt{\Delta x^2 + \Delta y^2 + \Delta z^2}}{\Delta t^2} $. And the second postulate of special relativity requires that the speed of a light particle/wave in a vacuum, so defined, is always equal to c.
No, there is no length contraction for the observer:
not perpendicularly (= vertically) because the observer is moving horizontally, thus length contraction may only happen in horizontal direction.
not in the sense of the observer's movement (= horizontally): For the simple reason that there is no observing reference system (!):
As you pointed out, the length contraction formula is
$D' = D \frac{1}{\gamma} = D \sqrt {1-\frac{v^2}{c^2}}$
D is the distance A-C from the point of view of the frame at rest with the distance (Instead of a distance you can also imagine a rod which has the length A-C).
v is the relative velocity of a third party observer (relative to the distance A-C/ the rod A-C).
D' is the contracted distance A-C from the point of view of this third party observer moving at v.
The horizontal distance is the distance between the observer and the lower mirror. From the mirror's point of view, the observer is moving towards the left. From the observer's point of view, it is the mirror who is moving to the right. By consequence, both are the two reference systems which are constituting the distance, and there is no third party which observes the length of the distance from an observing reference frame.
