What will happen if the potential is less than 0, for instance $V(x)=-10eV$. Is this means there will be no bound states? Since solution to the time independent Schrodinger equation (those discrete energies) must be greater than 0.
Asked
Active
Viewed 483 times
-1
1 Answers
1
Your finite square well potential looks like:
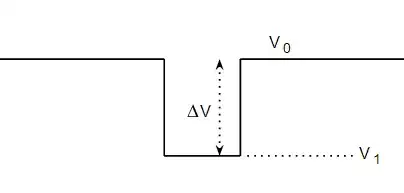
where $V_0$ is the potential energy outside the well and $V_1$ is the potential inside the well. The depth of the well is $\Delta V = V_0 - V_1$.
We normally take $V_0$ to be zero, in which case $V_1$ is negative (like your $-10$eV) and $\Delta V = V_1$. However you can add any constant value to the potential energies without changing the physics. That's because the wavefunction only depends on the well depth $\Delta V$, and adding the same constant term to $V_0$ and $V_1$ doesn't change $\Delta V$. We say the potential energy has a global gauge symmetry.
It's not clear from your question what you intended to have the value $-10$eV. You could set $V_0 = -10$eV and particles would still be bound in the well as long as $V_1$ was less than $-10$eV, that is $V_1 \lt V_0$.
John Rennie
- 367,598