Which way does the scale tip?

Question

I found the problem described in the attached picture on the internet. In the comment sections there were two opposing solutions. So it made me wonder which of those would be the actual solution.

So basically the question would be the following. Assume we would have two identical beakers, filled with the same amount of the same liquid, lets say water. In the left beaker a ping pong ball would be attached to the bottom of the beaker with a string and above the right beaker a steel ball of the same size (volume) as the ping pong ball would be hung by a string, submerging the steel ball in the water as shown in the picture. If both beakers would be put on to a scale, what side would tip?

According to the internet either of the following answers was believed to be the solution.

1. The left side would tip down, because the ping pong ball and the cord add mass to the left side, since they are actually connected to the system.
2. The right side would tip down, because of buoyancy of the water on the steel ball pushing the steel ball up and the scale down.

Now what would the solution be according to physics?

Answer 1

Here is a free body diagram of the balls:

… and one of the water volume:

The four balance equations are

$$ \begin{align} B_1 - T_1 - m_1 g & =0 \\ B_2 + T_2 - m_2 g & = 0 \\ F_1 + T_1 - B_1 - M g & = 0 \\ F_2 - B_2 - M g & = 0 \end{align} $$

where $\color{magenta}{B_1}$,$\color{magenta}{B_2}$ are the buoyancy forces, $\color{red}{T_1}$,$\color{red}{T_2}$ are the cord tensions and $M g$ is the weight of the water, $m_1 g$ the weight of the ping pong ball and $m_2 g$ the weight of the steel ball.

Solving the above gives

$$\begin{align} F_1 & = (M+m_1) g \\ F_2 & = M g + B_2 \\ T_1 & = B_1 - m_1 g \\ T_2 & = m_2 g - B_2 \end{align} $$

So it will tip to the right if the buoyancy of the steel ball $B_2$ is more than the weight of the ping pong ball $m_1 g$.

$$\boxed{F_2-F_1 = B_2 - m_1 g > 0}$$

This is the same answer as @rodrigo but with diagrams and equations.

Answer 2

The weight on the left bowl would be the weight of the water plus vase plus ping-pong ball (plus thread, ignored).

The weight on the right bowl would be the weight of the water plus vase plus the buoyancy of the steel ball (plus the buoyancy of the submerged thread, ignored). That buoyancy is the weight of an equivalent volume of water.

Since the ping-pong ball is lighter than water, the scale will tip to the right.

Why is that the weight on the right bowl? Look at it this way: the ball is in equilibrium, so the sum of all forces on it will be 0. These forces are weight, tension on the thread and buoyancy. So the tension on the thread is $tension = ball - buoyancy$ (obvious?). And the weight on the right plate is the sum of all weights minus the tension on the thread. That is $water + vase + ball - tension$, which is the same as $water + vase + buoyancy$.

Answer 3

A Thought Experiment

We can arrive at an intuitive explanation without any special knowledge of physics. The strategy is to re-create the setup as closely as possible while keeping the two sides in balance.

Imagine that you start with two identical beakers, filled with the same amount of water, no balls. Placed on the scale, they balance.

On the left, place a ping-ping ball with a thread dangling down. Let's pretend that the thread and the walls of the ball are of negligible weight. With that approximation, the scales remain balanced. (After all, all we have done is given a name to an arbitrary sphere of air above the water.)

Next, pretend that there is a water sprite at the bottom of the left beaker, operating a winch, tightening the string. Again, this has no effect on the scale, as the configuration change to the left beaker is self-contained. The ball sinks, and the water level rises.

On the right, lower a permeable ball into the water, suspended from a string. (Pretend that the walls of the ball are of negligible weight.) The ball fills up with water that was already in the beaker. Again, the scale remains balanced, since all we have done is given a name to an arbitrary sphere of water.

Suppose that there is a King Midas inside the right ball, turning water into gold, or steel, or whatever denser material. It makes no difference, since any additional weight will be borne by the string that suspends the right ball.

So far, the scales remain balanced. But what is the difference between the scenario so far and the one in your question? The water level on the right did not rise when we lowered the porous ball into the right beaker, the way it would have had we lowered a solid steel ball.

So, pour an amount of water in the right beaker equivalent to the volume of the steel ball, and you have recreated the setup! Of course, the scale would then tip to the right.

Answer 4

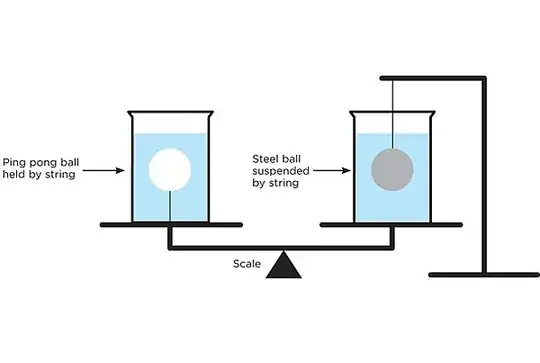
I'm amazed that this is so confounding to some. This is too long to be a comment, so I'm making it an answer. The TL;DR version: The answers that say the scale will tilt down to the right are correct. The beaker full of water with the steel ball suspended from above is heavier than is the beaker that contains the ping pong ball anchored from below.

Assumptions

• The two flasks are identical. To make this so, down to the splitting of hairs, let's attach a connector to the bottom of both flasks. The connector will be used to anchor the ping pong ball on the left to the bottom. We need that same connector, unused, on the right so as to make the flasks identical.
• The two flasks contain identical quantities of water.
• The ping pong ball and steel ball are the same size and are fully suspended in the water.
• The ping pong ball is less dense than water while the steel ball is of course more dense than water.
• The strings are of negligible mass.
• The scales are very sensitive and can detect differences in mass to the sub-centrigram level.

Experiment #1: Anchored ping pong ball on the left, no steel ball on the right

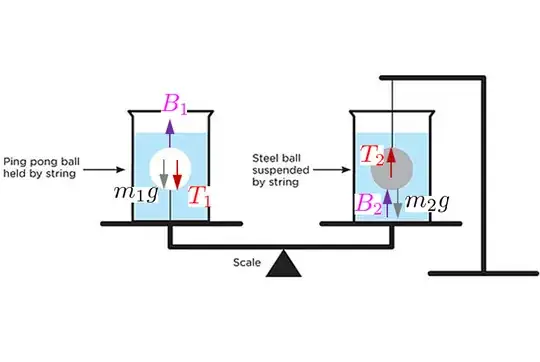
This one's easy: The left side is heavier. A simple explanation is to look at the water+ping pong ball on the left as a system. This system is static, so the net force is zero. The mass of the system is the sum of the masses of the water and the ball: $m_{w+b}=m_w + m_b$. Gravity exerts a downward force of $g m_{w+b} = g(m_w+m_b)$. Ignoring atmospheric pressure, the only other force is that of the bottom of the flasks on the water. This must exactly oppose the weight of the water+ball system to have a net force of zero. Thus the force transmitted to the left side of the scale is $W_l = g(m_f+m_w+m_b)$ where $m_f$ is the mass of the flask. On the right, there's only the mass of the water and the flask, so the force transmitted to the scale on the right is $g(m_f+m_w)$, or $g m_b$ less than that on the left. The scale tips down to the left.

Note that I ignored the forces on the string, buoyancy, and pressure. Invoking these results in the same answer as above, but with a lot more effort. The ball has three forces acting on it, gravitation ($W_b = g m_b$, downward), buoyancy ($B=g \rho_w V_b$, upward), and tension ($T$, downward). The ball is static, so $T+W_b = B$, or $T=B-W_b$. The water has three forces acting on it, gravitation ($W_w = g m_w$, downward), the third law counter to the buoyant force the water exerts on the ball ($B = g \rho_w V_b$, but now directed downward rather than upward), and the force by the bottom of the flask on the water ($F_p$ upward). The net force on the water is zero, so $F_p = W_w + B$. The forces on the bottom of the flask are the tension in the string, directed upward, and the pressure force from the water, directed downward: $F_f = F_p - T = (W_w + B) - (B-W_b) = W_w + W_b = g(m_w + m_b)$.

Some will say "but how does the reaction force to buoyancy transmit to the bottom of the flask?" Note that I didn't invoke Newton's third law in the context of the counter to the buoyant force eventually acting on the bottom of the flask. I used static analysis. The explanation of how this force is eventually transmitted to the bottom of the flask is via pressure. The force by the flask on the water is equal but opposite to the force by the water on the flask, and this is pressure times area. The presence of the ball raises the height of the top of the water by an amount needed to accommodate the volume of the ball, and this increases the pressure at the bottom of the flask. If the flask is cylindrical, this is a fairly easy computation: $\Delta h = V_b/A$, and thus $\Delta P = \rho g \Delta h A = \rho g V_b$. That's the magnitude of the buoyancy force.

Experiment #2: No ping pong ball on the left, suspended steel ball on the right

Now the scale will tilt down to the right. There's an easy way, a hard way, and a harder way to solve this. The harder way involves pressure, and the result will be the same as the other two approaches. I'll bypass pressure. The easy way is a static analysis. The water exerts a buoyant force on the ball, which exerts an equal but opposite force on the water. The water is static, so the bottom of the flask exerts a force on the water equal to the sum of its weight and the magnitude of the buoyant force: $W_w + B = g m_w + B$. Adding the weight of the flask gives the total weight on the right: $W_r = g(m_f + m+w) + B$. On the left, all we have is the weight of the flask and the water. The scale tilts down to the right.

Experiment #3: Anchored ping pong ball on the left, suspended steel ball on the right

Now we know the weight registered by the flask+water+ping pong ball system on the left and the weight registered by the flask+water+suspended steel ball system ob the right. It's a simple matter of comparing the two: $W_r - W_l = g(m_f + m+w) + B - g(m_f+m_w+m_b) = B - g m_b$. Since the ping pong ball floats, $B>g m_b$, so the scale tilts down to the right.

Experiment #4: Same as experiment #2, but now add water on the left

We can simply add water to the flask on the left in experiment #2 to make the scale balance. When we do that, we'll see that the scales balance when the water levels in the two flasks are at exactly the same height above the bottom of the flask. (This is the pressure argument.) If we measure the amount of water added, it will be equal in volume to the volume of the ball. (This is the buoyancy argument).

Experiment #5: Anchored ping pong ball on the left, left flask from experiment #4 on the right

Since the two flasks in experiment #4 have the same weight, the scale will still tilt down to the right, just as in experiment #3. If we look at the two flasks, we'll see that the water level in them is the same.

Experiment #6: Anchored ping pong ball on the left, anchored crushed ping pong ball on the right

Here we replace the steel ball in experiment #3 with a crushed ping pong ball anchored from the bottom. Since the buoyant force cancels out in the ping pong ball+water system (see experiment #1), one might think that the intact versus crushed ping pong ball test will balance. That is not the case. The intact ping pong ball weighs a tiny bit more. It has about 4 centigrams of air inside it. This is part of the measurement on the left but not on the right. The system with the intact ping pong ball is slightly heavier. Since our scale is accurate to the sub-centigram level, the scale will tilt down to the left in this experiment.

The above is incorrect. The water level will be a bit lower on the crushed ping pong ball side. Unless ping pong balls are inflated to considerably more than atmospheric pressure, the slightly increased pressure on the crushed ping pong ball side will more or less compensate for the reduction in mass.

Experiment #7: Replace the steel ball in experiment #2 with an intact ping pong ball

Finally, let's replace the string attached to the tower that suspends the steel ball in the water with a rigid rod attached to the tower that forces a ping pong ball to be immersed underwater. The result will be identical to experiment #2. The buoyant force is equal to volume, not mass. It doesn't matter what kind of ball we use so long as the volume remains the same. The effect on the tower will of course be markedly different, but the tower is not a part of the systems we are weighing.

Answer 5

Well I got this badly wrong, and grovellingly apologise to those I traduced.

It seemed easy: the water in both is the same weight, so I thought that removing it would make no difference to the balance. This was wrong: removing the water from the right hand beaker does have an effect, the presence of the suspended ball does add extra weight to it, so the right hand pan descends.

I did some experiments to check this out, using a plastic drinking cup on a sensitive digital weighing scale, I was limited by the maximum weight the scale would show, to 200 gm total, which constrained how I did the tests. I photographed the results (apologies for the backgrounds, ignore the green label) :

. The first photo (top left) shows the cup with water and a piece of plastic tethered to the bottom of it. The second (top right) has the plastic removed and hung on the rim of the cup, above the water and shows that there is no difference in the weight. This was what I expected. The third image (bottom left) shows the water alone (the hook came off and I discarded it) , note the weight, and the final photo has a 100 gm steel test weight suspended in the water, and, to my initial surprise, the weight shown on the scale has gone up. So the correct conclusion is that the right hand pan will descend.

As a final experiment, not photographed, I noted the water level and scale reading before I lowered the steel weight in. After I lowered the weight under the surface I removed water back to the same level. That is I removed the water that was displaced by the weight, and the scale reading went back to the original. To me this shows that the additional weight on the pan when the heavy mass is submerged, is equal to the weight of the water displaced.

This leads to a simple explanation of why the right hand pan dips. Remove the steel ball and imagine it leaving behind a hole in the water exactly the same size as the ball, so that the overall level of the water surface is what it was with the ball still immersed. Picture this hole filling up with extra water: then the forces on the spherical blob of water that has replaced the ball are exactly the same as those that acted on the suspended ball. To me this shows that the presence of the ball adds a weight equal to that of the volume of water displaced.

It also shows that the only two things that matter about the suspended object are its volume, and that it is more dense than water. Its weight and shape are immaterial (so long as it does not trap any additional air as it is lowered below the surface.)

I realise now that something very similar has been said in comments and answers already given, and although I arrived at this on my own, I appreciate and acknowledge their prior insight.

Answer 6

For some height $h$ of the liquid, the pressure of the water on the bottom of the beaker is $P = h \rho g$ where $\rho$ is the density of the water*. Since $h$ is the same for both beakers, $P$ is the same.

Net force on the bottom of the left hand beaker is sum of the water pressure $PA$, minus tension of string pulling on the bottom:

$$F_{left} = P A - T$$

On the right hand side, the only force on the bottom of the beaker is

$$F_{right} = P A$$

The difference is the tension in the string: as long as the tension is positive (that is, the pingpong ball would float if we cut the string), the right hand side will tip down.

---

* Note - further to comment below (which may disappear), I do mean "density of the water", and not "effective density of water which is lighter because mass / volume is smaller as there is a bit of volume without water in it". That is just how hydrostatics works: the pressure will be that caused by the column of water, and it will be the same at every point along the bottom. To state otherwise is to perpetuate the confusion.

Answer 7

my answer is the beaker with steel ball will tip down although my explanation may sound weird :

it's not through mass and buoyancy , it's through pressure and buoyancy

1- the water pressure at both beaker's floor equals water height x the beaker floor area and they are equal

2- there's nothing attached to the beaker on the right that would push it down or upward

3- there's a ping pong ball attached to the beaker on the left that want to go upward.

bonus puzzle : what happens in the first few milliseconds if we cut both strings at the exact moment ?