Which way will the scale tip?

Question

This problem has bothered me for quite some time and I can't solve it. I have even tried to make a construction, but it sometimes tips to the left and sometimes tips to the right :).

When we submerge the body in the water the water pushes it up. That is an action. At the same time the body pushes water down. That is a reaction. So the balance should be maintained.

But, since the water level rises the hydrostatic pressure on the bottom is greater so the right side should go down.

There is another similar problem but it's not the same.

Please help.

Answer 1

The scale will not move.

You don't need to think about buoyancy at all to answer this question. In the first picture, the scale is balanced, because the net force on each side (the weight) is equal. No mass is added to or removed from either side, so the net forces remain the same.

Answer 2

The balance will be maintained because there is no EXTERNAL force applied on left or right side. This is because of the same reason you can't push a car while sitting in it!

Answer 3

So various forces neglected (including gravity, air resistance, thermal forces, air pressure) - but your question suggest this is an inquiry about the effect of bouyancy.

That being the case, lowering the mass into the water brings into effect its bouyancy. This is a force lifting the mass and acting down on the water. However, as the mass is tethered to the scale the force acting down the string is reduced by the same amount as the bouyancy, and the net effect on the scale is zero.

(Also neglecting rotating frames of reference, light pressure, stress and young's modulus, magnetically induce currents etc)

Answer 4

If you consider everything put in the right side of balance scale as one system, only the internal forces are changed which will not affect the balance. No external force is applied and hence the balance will be maintained.

Answer 5

Let $V$ be the volume of the hanging block, $A$ the area of the water surface, $\rho$ the density of water, and $g$ the acceleration due to gravity.

The extra hydrostatic force felt by the bottom of the container after lowering the block is $$\Delta F = \rho gA\Delta h,$$ where $\Delta h$ is the change in water height ($\rho g \Delta h$ would be the change in hydrostatic pressure). Because water is not compressible, $A\Delta h$ must be the volume of the submerged block. $$\Delta F = \rho g V.$$ Notice that this is exactly equal to the buoyant force on the block, so the two new forces created after the block is submerged negate each other.

Answer 6

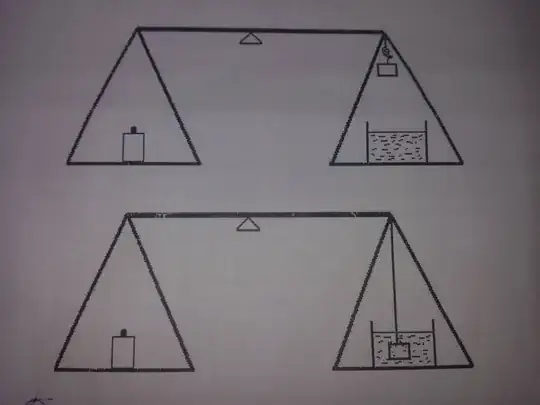
EDIT:

Since this answer is not being very well received I will just say that if we neglect gravitational forces due to the height difference between the mass in the upper and lower pictures; then yes, the scales will be balanced as there is simply no net torque.

---

However, since the question did not stipulate these assumptions then the answer below is the correct one:

Look at the RHS of the scale and consider Newton's Law of Gravitation $$F=-\frac{G \cdot m\cdot m_E}{d^2}$$ On the RHS consider $m$ to be the mass of block suspended by the string and $m_E$ is the mass of the Earth $\approx 6\times 10^{24}$kg. $G$ is the gravitational constant and $d$ is the distance of the string between the block in the top picture and the one in the bottom plus the distance to the centre of the earth.

Now let $m_{s}$ be the mass of the submerged block in the container of the lower RHS and $d_E$ is the distance to the centre of the earth. $$F=-\frac{G \cdot m_{s}\cdot m_E}{d_E^2}$$

The gravitational force acting on the RHS of lower system is therefore greater by Newton's inverse square law.

Can you now understand why once the block is dropped into the fluid the RHS of the lower image will weigh more and hence tilt clockwise?