3

I was pondering Which way does the scale tip? I understand it tips to the right. Here's the setup:

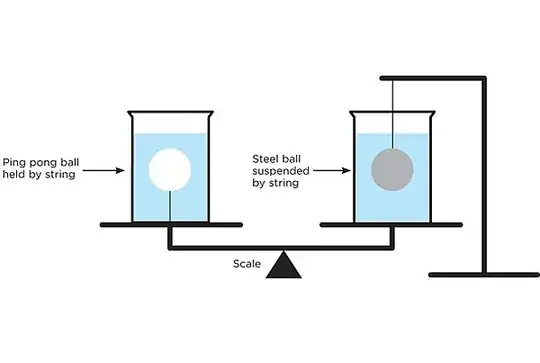
The issue is my intuition fails in understanding what happens on the right side. If I place a beaker with water on a scale, it will measure some weight. And if I then suspend a steel ball in that water, the scale will measure a greater weight, even though the ball is suspended by something else. Seems like magic.

Intuitively, I can look at this problem from two perspectives:

  1. As the stand
  2. As the scale

As the stand, it makes sense. I've carried weights into swimming pools and felt them become apparently lighter. I'm told this is due to "buoyancy", but I'm not sure I intuitively understand it. It feels easier to accept though, since I have experienced it directly.

But starting from the perspective of the beaker, how does this make any kind of intuitive sense? From this perspective, I think the volume of water in the beaker, which I am supporting, has not changed. I just can't conceive of how suspending a weight in the water could possibly change anything.

If I look at the whole system, it's apparent that if the steel ball is apparently lighter, then whatever the scale is supporting must be apparently heavier by an equal amount. But this doesn't satisfy me as an intuitive explanation: I know this must be true mathematically, but without being able to understand from the perspective of the scale I don't know why it's true. What's it like to be the scale in this setup, intuitively?

Community
  • 1
Phil Frost
  • 4,241

4 Answers4

4

It may be easier to understand if you think about the pressure inside the water and the forces that the water exerts on the sphere and the bottom of the beaker. First of all remember that pressure p increases with depth inside the water according to

$$p = \rho gh$$

where $\rho$ is the density, $g$ is the gravitational acceleration and $h$ is the depth. The force exerted on a surface is the pressure multiplied with the area of the surface.

When you lower the sphere into the water, the water level rises. This means that the pressure at the bottom of the beaker increases because $h$ has increased. Due to this increase in pressure, the downward force of water on the bottom of the beaker has increased, pushing the scale down.

Now you might ask where this force comes from because the weight of the water has not increased. Again due to the pressure increase with depth, the water pushes more against the bottom facing surface of the sphere than against the top facing surface. This is because the top facing surfaces are higher up in the water than the downward facing surfaces. According to the law of action-reaction this means that the sphere is effectively pushing down on the water.

One can show that these two downward forces are exactly the same. You can do the calculations for a cylindrical weight using school maths. For arbitrary shapes it is still possible to show but one will need some advanced maths.

Holger Schmitz
  • 404
2

I think this is not intuitive to you because you are not differentiating between mass and weight. The mass of the system has not changed; there is still that same amount of water there as before. The weight of the system has changed. The weight would be the force of the water due to gravity. Now since we are increasing the the pressure of the water (which is just force over area), there are "extra forces" (not just the ones due to gravity). The summation of these forces is greater then the original force (the force of gravity alone). Therefore the systems weight has changed.

student.q
  • 69
0

well it is beause water is oposing the steel ball from entering. This push makes the ball appeare lighter and it is what makes the hole system heavier.

Žarko Tomičić
  • 1,835
0

You can explain this intuitively bu saying that whatever force the liquid applies on the steel ball, the same force(magnitude but opposite direction) is applied on the liquid by the ball(newtons third law). Now if you take both the ball and the liquid as a system and examine the forces acting on the system, you can see that these 2 equal and opposite forces cancel and the scale has to bear the weight of both the liquid and the ball. Hope this helps.

lifelong_student
  • 129