Both the basketball and the medicine (steel) ball are the same size, which means they're displacing the same amount of water. That should mean the buoyant force is the same on both, right? But then why does one side of the scale tip more than the other? I'm trying to figure out what extra force is acting here that the scale can "feel" — because it seems like the water should cancel things out.
The important point is that internal forces cancel out. Therefore, it can immediately be concluded that the weight of the system on the right is simply the sum of the container, water and basketball.
Similarly, for the system on the left, without the string, its weight will be the sum of the container, water and steel ball. But the string exerts an external force equal to the difference in weight between the steel ball and an equivalent volume of water. Subtracting off this difference from the weight, it can be seen that the weight felt by the scale becomes the sum of the container, water and the equivalent volume of water i.e. that of an identical container filled to the same level with just water.
Therefore, since the basketball is less dense than water as shown by the taut string, it weighs less than the equivalent volume of water. The system on the left is heavier.
The free body diagrams are as shown below.
The steel ball forces add up to zero as do the basketball forces.
The downward force on the scales is $M_{\rm w} g+U$ for the steel ball arrangement which is greater than $M_{\rm w} g+U-t$ for the basketball arrangement.
First consider what happens with no strings attached (no pun intended).
The downward force on each side of the scale will simplify be the weight on each side. The weight on the left is greater than the right (assumes same cups and volume of water) and the scale will tilt down on the left. The buoyant forces are internal to the ball/water/cup system and therefore have no effect on the weight of each system with no strings attached. Therefore, with no strings attached, the scale will tilt down on the left.
Now consider the effect of the strings.
The tension $T$ in the string on the left is an external force on the ball/water/cup system. It therefore lessens the downward force on the scale on the left according to the following where $W_{MB}$ is the weight of the medicine ball
$$W_{left}=W_{MB}+W_{H2O}+W_{cup}-T\tag{1}$$
The tension on the left makes the net force on the medicine ball of zero. Thus the tension equals the weight of the medicine ball minus the upward buoyant force, or
$$T=W_{MB}-F_{b}\tag{2}$$
Substituting (2) into (1)
$$W_{left}=W_{H2O}+W_{cup}+F_b\tag{3}$$
The tension in the string on the right, which is attached to the bottom of the cup, is an internal force of the system. Therefore it does not effect the weight on the right. But the weight of the ball component of the ball/water/cup system and the buoyant force will determine the tension. The weight on the right side, where the weight of the basketball is $W_{BB}$, is
$$W_{right}=W_{BB}+W_{H2O}+W_{cup}\tag{4}$$
The scale will be balanced if the weight on the left equals the weight on the right, or
$$W_{BB}=F_b\tag{5}$$
But equation (5) is the equivalent of stating that for the scale to be balanced, the weight of the basketball must equal the buoyant force acting on it, i.e., the density of the basketball equals the density of the water displaced by the ball. That in turn means the basketbal can can float completely submerged without the need of the string, i.e., the tension in the string would be zero. For there to be any tension in the string, the basketball would need to weigh less, which in turns would make the total weight on the right side less. From that we can conclude that if there is any tension in the string on the right, the scale will necessarily tilt down on the left.
Hope this helps.
Buoyancy doesn't remove weight. Throw a ball into a cup and, even if it floats, the cup will feel heavier. The two balls feel the same buoyancy, but the left-hand container is still heavier, because the density of steel > the density of the basketball.
To clarify: for the steel ball, we can write the forces acting as $T + \rho g V = mg$. For the basketball, it is $m'g + T' = \rho g V$. Both of these must balance, since the balls aren't moving. The water exerts the full $\rho g V$ on the steel ball. By Newton's third law, the ball exerts the full $\rho g V$ on the water as well (and by extension the scales).
The water also exerts the full $\rho g V$ on the basketball, but because this buoyancy is > the basketball's weight, there is also a tension in the string holding the basketball underwater that reduces the weight on the scales.
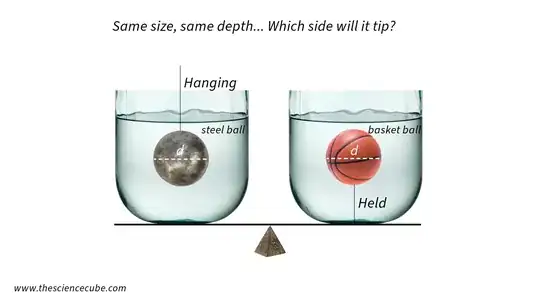
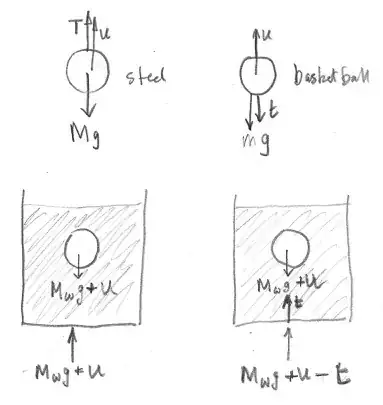
The difference is the anchoring points, as others have said.
It helps me in these cases to just remember that the principle of buoyancy is a special case of the minimization of potential energy in static equilibrium. Consider that the left cup goes up and the right cup goes down by a millimeter, how has the energy changed? Assume that the rounding of the cups doesn't matter as if there were no balls the two would balance, so idealize those as perfect cylinders with some cross section area, say, $400\text{ cm}^2$, filled up maybe to $30\text{ cm}$. The balls inside are size-3 mini basketballs with a radius of $8.9\text{ cm},$ the steel being some 23 kilos and the normal one being 280 grams.
You can do this in two ways, "teleporting water" analysis or actual equations. If you analyze buoyancy by teleporting water, then when the cup holding the steel ball moves up by a millimeter, a volume of $0.1\text{ cm}\times400\text{ cm}^2=40\text{ mL}$ needs to be deleted from the bottom of the cylinder and then re-added at the top of the cylinder, it has “teleported” up by $30\text{ cm}.$ But on the right a separate $40\text{ mL}$ is displaced downward by $30\text{ cm}$, and these two effects cancel in terms of energy. And this is why if there were no balls, the scale would balance.
However, what changes with the ball on the right is that the steel ball on the left doesn't move but the basketball on the left has also dropped $1\text{ mm}$. The ball has some mass which lowers the energy, but it also will sweep out its cross section of $\pi r^2$ (roughly $250\text{ cm}^2$) for a millimeter and that water has to be teleported upwards as it sinks downwards, by an average distance $\frac43 r$ (roughly 12 cm). So you have 280 grams of basketball moving down by one millimeter, energy change roughly $-2.8\text{ mJ}$, but balanced out by 25 grams of water teleporting up by 12 centimeters on average, energy change roughly $+3.0\text{ mJ}$, and we know that the second number is always greater (in absolute value) than the first number because if it weren't, the ball wouldn't float in the first place.
Energy minimization therefore says that the floating basketball will pull its side up with its buoyant force, the steel ball will not push its side down with the same because it is suspended and unable to fall to reduce the potential energy.
In equations, we have the left hand side sitting at vertical position $+y$, the right hand side sitting at $-y$, the potential energies on the left and right are, $$ U_L = \rho g\left(\pi R^2 h~\left[\frac{h}{2} + y\right] - \frac43\pi r^3~\frac{h}{2}\right) + m_\text{Steel} g \frac{h}{2},\\ U_R = \rho g\left(\pi R^2 h~\left[\frac{h}{2} - y\right] - \frac43\pi r^3~\left[\frac{h}{2}-y\right]\right) + m_\text{Basketball} g \left[ \frac{h}{2}-y\right].$$
It's a lot to write but you can see the above analysis poking through: when we form $U=U_L+U_R$ the leading $\pi R^2 h$ terms will add together to lose their y-dependence, and then when we compute the force the $\frac{dU}{dy}$ terms also disappear completely, leaving just $\frac43\pi r^3\rho-m_\text{Basketball},$ which is just the criterion for whether the basketball floats or sinks.
Both cups have the same amount of water in them. Weight of water is thus equal.
The two balls have the same volume, so the buoyancy of both is the same. Weight of water displaced are the same.
The wire holding the medicine ball will provide $T=\,$weight of medicine ball - buoyancy. This means that on the left side, the scale is holding up cup of water + displaced volume of water. This is equivalent to having no ball there but with the ball's volume replaced by water.
On the right hand side, the basketball is held down by a string tied to the bottom. Clearly this string is pulling down the basketball, and it can only do that by pulling up on the cup. The cup thus weighs slightly less, hence the tilt.
The left balance beam with the steel ball will go down! This is very easy to see.
The water volume and weight in both containers is the same. Thus it is the difference in the forces on the immersed equal volume steel and basket ball that determines which side goes down.
On the right balance beam, the basket ball is attached to the bottom of the container. Thus there is no effect of the internal force of buoyancy of the basket ball on the right balance beam. The total external force acting on the right beam is just the sum of weights of the container, the water and the basket ball.
The total external force on the left beam is the weight of the container and the water, which is equal to the right container, plus the external force on the water exerted by the immersed hanging steel ball. According to Newton’s third law, this force must be opposite to the buoyancy exerted by the water on the steel ball, which, according to Archimedes, corresponds to the weight of the displaced water. The weight of the displaced water is obviously larger than the weight of the equal volume basket ball.
Therefore the total downward force on the left balance beam with the steel ball is larger than the force on the right balance beam with the basket ball.
Notice the difference in how the tether that holds the ball in position is secured.
The fluid container with the basket ball:
the tether is secured to the fluid container.
The fluid container with the steel ball:
the tether is secured to something other than fluid container.
So between left hand side and right hand side there are two differences that affect the outcome.
In order to make a comparison the second difference must be removed.
The two options:
