I have always wondered and once I even got it, but then completely forgot. I understand that gravity causes high and low tides in oceans, but why does it occur on the other side of Earth?
8 Answers
Imagine that we have a very massive object in space. At some distance away (call it ten units) we release three tennis balls in a row:
The tennis balls all fall towards the massive object. But because gravity goes like distance squared, the nearer balls feel a stronger attraction than the farther balls, and they move apart from each other:

You're riding on the middle tennis ball. You feel like you're in free fall, in a good inertial frame. You look towards the heavy object and you see the leading tennis ball moving away from you. You look away from the heavy object and you see the following tennis ball moving away from you. The heavy object is pulling the three tennis balls apart.
Likewise, if you had three objects at the same distance falling towards the massive object,

you'd see them converge as they all fell along slightly different rays towards the same center. This gives the tidal compression. You can imagine the process of launching a whole constellation of tennis balls, choosing the center one as your "rest frame," and having their motions approximate the arrow pattern in Joshua's figure.
The situation stays essentially the same if you add angular momentum, except that then your tennis ball constellation doesn't crash onto the massive object.
First we must understand a little what is meant by "tide." A tide is the difference of gravitational force an object feels across its volume from another object. In the Earth's case the side closest to the moon feels a stronger force pulling it towards the moon than the center of the Earth does, while the side opposite the moon feels a force weaker than the center of the Earth feels. The picture below (taken from this site, which is a great reference as well, especially for explaining some misconceptions about the second lunar tidal bulge) shows this. The center of the earth feels a force toward the moon as calculated by Newton's Law of Gravitation:
$$F=G \frac{m_1 m_2}{r^2}$$
while the other areas of the Earth's surface feels a slightly different force from the moon than the center of the Earth does, as demonstrated by the arrows. The side closest to the moon feels an additional force by virtue of being closer to the moon, as demonstrated by the arrows pointing towards the moon, while the side furthest away feels a less strong force, represented by the arrows pointing away from the moon (here represented as a generic satellite).

The side closest to the moon has a tidal bulge because of the additional gravitational force pulling the sea level higher than the average level, while the side opposite the moon also has a tidal bulge by virtue of the lessened force of gravity it feels being further away from the moon. So, both bulges are caused by the moon; one side feels a greater attraction, while the other side feels a smaller attraction.
- 103
- 5,473
The Earth is free falling towards the Moon. Because gravity decays with distance, the side near the moon wants to fall faster than the center of the Earth, while the other side tends to fall slower. So observed on the Earth, the other side "lags behind" and therefore we have high tide there.
- 5,473
- 4,064
Let us try to find the acceleration at points A and B with respect to the centre of the earth O due to the influence of moon and earth, as shown in the figure.
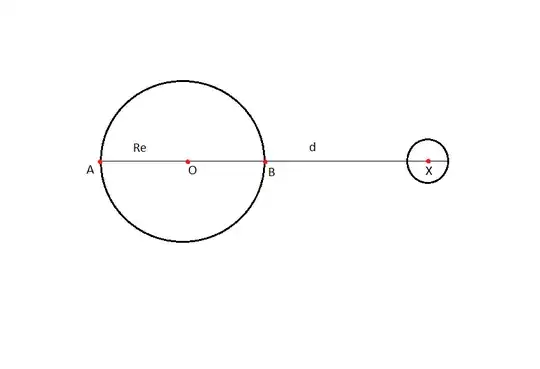
O and X are the center of the earth and moon respectively. Let the radius of earth be $R_E$, distance between earth and moon be $d$, mass of earth and moon be $m_E$ and $m_M$ respectively. $O$ to $X$ is taken as the positive direction. I have assumed $R_E << d$.
Acceleration of point B $a_B$ is:
$$a_B = -\frac{Gm_E}{R_E^2} + \frac{Gm_M}{(d-R_E)^2}$$
$$= -\frac{Gm_E}{R_E^2} + \frac{Gm_M}{d^2}(1+ \frac{2R_E}{d})$$
Similarly, $a_A$ is:
$$a_A=\frac{Gm_E}{R_E^2} + \frac{Gm_M}{(d+R_E)^2}$$
$$=\frac{Gm_E}{R_E^2} + \frac{Gm_M}{d^2}(1-\frac{2R_E}{d})$$
And $a_O$ is:
$$a_O = \frac{Gm_M}{d^2}$$
Thus, the accelerations of point A and B with respect to O are:
$$a_{AO} = a_A-a_O = \frac{Gm_E}{R_E^2} - \frac{2Gm_MR_E}{d^3}$$
$$a_{BO} = a_B-a_O = -\frac{Gm_E}{R_E^2} +\frac{2Gm_MR_E}{d^3}$$
But now, we get $a_{BO}=-a_{AO}$, which means that on both the sides, water will be trying to move away from the centre of the earth, thus causing tides on both the sides of the earth.
Citation: Bennett, Robert. The Geocentric Testimony of our Tides: A brief study of the near and far side effects of gravity. 2018.
- 103
- 1,108
- 10
- 26
This is because the gravitational field of the Moon, like any object, is not uniform - in particular, closer to the Moon it is stronger, and further away it is weaker. With regard to the Earth, the side of the Earth that is closest to the Moon experiences a slightly stronger pull than the side further away, which effectively results in the Earth being "stretched" ever so slightly as the nearer side accelerates harder than the farther side in response - and when you stretch an elastic sphere it becomes an oblong with a bulge on each side and not just on one side like a pear (as I imagine you'd be thinking it would have to look.).
From the viewpoint of the Earth's center of mass, which is being accelerated by this effect and may be more natural for you, the reference frame change results in the side of the Earth closest to the Moon as experiencing a force toward it, and the opposite side experiences a "fictitious" force directed away, thus creating a stretch in both directions - this opposite fictitious force because that frame is not inertial, just as with driving in your car how there is a "fictitious" force when you slam the gas that wants to push you into the seat and throw the bobblehead off the dashboard.
In a uniform gravitational field, this effect does not occur. The difference in forces that produces the stretching is called, perhaps not unsurprisingly, a "tidal force".
Also, if one has read any pop sci books or seen movies about "black holes" and they've talked about getting "pulled apart like spaghetti" when you fall in because the force on your feet is higher than that on your head, that is exactly this effect but much more extreme - and conversely, this effect is a very, very incipient form of the "spaghetti pull" effect manifested over a far larger distance due to the much gentler gravitational gradient.
- 20,929
A two-dimensional model seems quite helpful for understanding. This is shown in the following picture.
The moon is modeled as a point mass on the right, denoted by letter $m$. To see that there are tides at $A$ and $B$, one need to show that in the reference frame fixed on the earth, the apparent acceleration one experiences at $A$ and $B$ toward the center of the earth "$e$" is smaller than, say, that at the reference point $R$.
For simplicity, take the moon and the earth to be rotating around the center of mass "C" in a circular orbit with $|em|=r_r$. The earth may or may not be rotating by itself. When calculating the accelaration toward the center of the earth $e$ for the points $A$, $B$ and $R$ respectively, the gravitational pull due to the earth and the centrifugal acceleration due to earth's own rotation are all exactly the same, so one may disregard them from here on.
At point $A$, the acceleration toward $e$ is due to the moon's gravitational pull and the centrifugal effect due to the orbital rotation of the earth and the moon around each other (disregarding earth's gravitational pull and the centrifugal acceleration due to earth's own rotation as mentioned above): $$-G \frac{m_m}{(r_r-r_e)^2}+\omega_o^2 r_r \frac{m_m}{m_m+m_e}\\ =-G \frac{m_m}{(r_r-r_e)^2}+G \frac{m_m}{r_r^2},$$ $$\sim -2 G \frac{m_m r_e}{r_r^3}$$ where $\omega_o$ is the orbital angular velocity of the moon relative to the earth, $r_e$ is earth's radius, and use has been made of the familar relation $\omega_o=\sqrt{\frac{G (m_e+m_m)}{r_r^3}}$.
Similarly, at point $B$ the acceleration toward the center of earth is $$ G \frac{m_m}{(r_r+r_e)^2}-G \frac{m_m}{r_r^2}$$ $$\sim -2 G \frac{m_m r_e}{r_r^3}$$ Note that at both $A$ and $B$ the acceleration due to the orbital rotation of earth and moon around each other is the same $G \frac{m_m}{r_r^2}$ and both toward the $-x$ direction. Consequently, when calculating the acceleration toward the center of earth $e$ at $A$ and $B$, they appear with opposite sign.
At the reference point $R$, the centrifugal term due to orbital motion does not contribute while the moon's gravitational pull leads to: $$G \frac{m_m r_e}{(r_r+r_e)^{3/2}}.$$ Comparing the three formulas for $A$, $B$ and $R$, one sees that the apparent accelerations toward the earth center $e$ are the same and negative at $A$ and $B$, while is positive at $R$. This means there are two tides, at $A$ and $B$.
- 455
I tried it this way, without comparing it with free-falling objects. Consider two spherical masses, a big one with mass $M$ and radius $R$, and a little one with mass $m$ and radius $r$. The distance between the centers of the spheres is $l$. They revolve around their center of mass (given by $\frac {l}{1+\frac{M}{m}}$) with an angular velocity of $\Omega$. M is rotating with angular velocity $\omega$. The rotation speeds lie in the same plane.
If I calculate the forces acting on opposite sides of $M$, on the line between the centers of the masses, and compare them with the case in which no $m$ is present we can see what happens if water were present on $M$.
For the far side on $M$ we have these forces:
$F_{cf\Omega}$, the centrifugal force due to the rotation of $M$ around the CM.
$F_{cf\omega}$, the centrifugal force due to the rotation of $M$ itself.
$F_{gM}$, the gravitational force from the sphere we are looking at, directed towards the center of $M$
$F_{gm}$, the gravitational force from the other sphere, directed towards the center of $m$.
Let's start with the total force on a test mass (which we make 1$kg$) on the opposite side which is, of course, the sum of all the forces, which are (cf means centrifugal):
$$F_{cf\Omega}=-\frac{v^2}{CM+R}=-{\Omega}^2 (\frac{l}{1+\frac{M}{m}}+R)$$
and because of ${\Omega}^2=\frac{G(M+m)}{l^3}$
$$F_{cf\Omega}=-\frac{G(lm+R(M+m))}{l^3}$$
$$F_{cf\omega}=-\frac{{v'}^2}{R}=-{\omega}^2{R}$$
$$F_{gM}=\frac{GM}{R^2}$$
$$F_{gm}=\frac{Gm}{(l+R)^2}$$
Suppose $\omega=0$. In this case, the centripetal force $F_{cf\Omega}$ (directed away from $m$ on the line $l$ (hence the minus sign) is bigger than the combined gravitational force on the test particle exerted by $M$ and $m$. So if water were present on the far side of $M$ the water would experience less force. Hence a bulge. When $\omega$ has a positive value, the total centrifugal force will be even bigger, and so will be the bulge.
On the opposite side (on $M$, the closest to $m$), the centrifugal force due to $\Omega$ pushes the water to the ground but the combined gravitational force of $M$ and $m$ is pulling the water away from $M$ with a greater force so a bulge of water develops on this side too. If $\omega$ is non-zero the associated $F_{cf\omega}$ will, in this case, make the bulge bigger too as it is this case directed towards $m$ instead in the opposite direction.
This holds for masses with perfectly smooth surfaces. For surfaces like the Earth (form 11$km$ below the water surface to 9$km$ above the water surface, the rough surface will distort the two-sided bulge in chaotic ways. The water flows in this case in mysterious ways. The rotation of the Earth makes the bulges even more distorted.
- 1
- 5
- 45
- 105
Another way of picturing the answer is by considering that earth rotates around the same point as does our moon. If the moon had the same mass as the earth this point would be halfway between the two bodies. As the moon is much lighter than earth the centre of rotation is much closer to our planet but it is outside earth's surface. Because earth rotates around this Centre of Gravity, all parts of it experience varying centripetal forces. Solid and liquid matter on the part of earth surface that is furthest away from the CofG have the highest forces, matter nearest the CofG has the least while in between there is a gradient of magnitudes. So water on the far side is forced out the most, on the nearside the least and the solid in between somewhere between the two. So two bulges, although not quite in line with the moon because of restrictions to water flow (friction). When the sun and the moon are on the same line as earth the tides are higher.
- 7
