Relative size of the 2 tidal bulges

Question

I am interested in making a simplified model that represents only the effect that the moon has on Earths tides. In this model I am going to assume that the earth is completely spherical (with no continents or surface variation) and covered entirely by a single ocean of water.

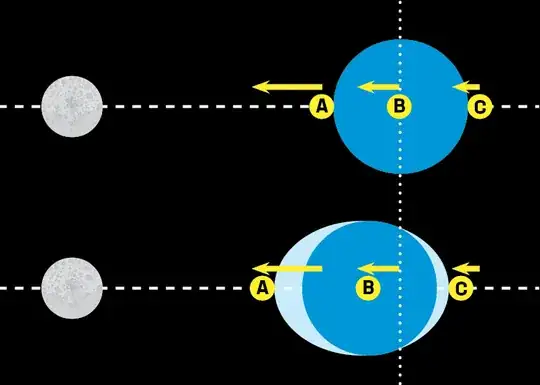
In simple terms I want to know if the tidal bulges on the earth are different sizes or if they are of equal size?

In many diagrams it appears that the bulges are symmetrical, but if the side of the earth facing the Moon is experiencing a greater gravitational force, and the far side a weaker gravitational force, would that not result in the side facing the Moon having a proportionally larger tidal bulge?

I do appreciate that most diagrams are purely illustrative and that the actual difference in size would be too small to practically depict on a visual diagram.

I have attached a diagram, that while exaggerated, I am wondering if it is more accurate that showing the bulges as equal in size?

Answer 1

Yes, to some degree, but not for exactly the reason you're imagining.

Even in the idealized model you're using, the size of the tides is not controlled by the strength of the moon's gravitational pull at $A$ and $C$, but by the difference in the moon's gravitation between $A$ and $B$, or between $C$ and $B$.

This difference in gravitation between two neighboring points fall off proportionally to the inverse cube of distance rather than inverse square of the graviational field itself.

Since the moon is about 30 earth diameters away, we would expect the tidal effect to be about one part in 90 less on the far side of the earth.

---

In reality the "tidal bulge" model is very inaccurate for explaining how the oceans rise and fall. It is more accurate to consider the oceans as a very complex driven oscillator, where the water is slowly sloshing around. The periodic minor variations in gravity caused by the moon contribute energy to the sloshing, but the actual shape and timing of the sloshes is much more influenced by coastlines than than by the moon itself.

Indeed tides in the earth's oceans do have a component with a period of 25 hours (the approximate time from moonrise to moonrise) as well as the more well-known component with a period of 12½ hours. In some places (such as the Gulf of Mexico) the 12½-hour mode almost vanishes, such that even though it is driven at 90 times the strength globally, the amplitude of the 25-hour oscillation dominates locally. This leads to diurnal tides.

Answer 2

The strength of the gravitational force falls off like the square of the distance, $r^{-2}$.

Tides arise because the gravitational force on an extended object is stronger on the near side than it is on the far side. That difference goes like the rate of change of the force, so the tidal stretching goes like $r^{-3}$.

An asymmetry in the tidal force would take place if the tidal stretching on one side of your extended object were larger than the stretching on the other side. The size of this asymmetry would vary like the rate of change of the strength of the tidal force, or like $r^{-4}$.

So yes, there should be such an asymmetry. But if the magnitude of the tidal stretching is small compared to the gravitational force, the magnitude of the asymmetry will be small compared to the tides by kind of the same factor.

Answer 3

I have to say that the premise of the question doesn't make complete sense to me. You say you're trying to isolate the effect that the moon alone has on the tides, but without taking inertia into account? The inertia of the Earth is what creates the tide on the opposite side, no?

The included picture at the top looks essentially like what would happen if the Earth and moon had no velocity... yes that might create a far tide by virtue of the water on the far side being pulled slower than the Earth, but that doesn't have any bearing on how the actual far tide is created.

In fact, the Earth, swings AWAY from the Moon's gravity (due to their orbit) creating an inertia that causes the tide on the far side -- it's not due to some stretching of the water towards the moon across the Earth, that's kind of a misconception.'

EDIT: Also, Jeb I was confused by a different comment you made: "The tidal budge model would lead to smaller tides at higher latitude, and max tides at the equator. Proof? Look at the picture. Of course, reality is the opposite--now why that arrises from the driven oscillator model idk. This argument always got me in trouble in grade school (long before wikipedia)."

But the Earth spins on an angle. The actual sides that face the moon are rarely along the actual equator. In other words, if the Earth were spinning straight along our north-south axis, then yes, the equators would bulge due to the tides. So that's another reason I have an issue with the picture you included.

Answer 4

The tidal force on the point on the earth nearest to the moon, is roughly 1/20 greater than than on the point furthest from the moon, which is what I think was being asked, not 1/90 as stated in the other answer.

The moon is roughly 60 earth radii from the earth, so if we call the gravitational force of the moon on the centre of the earth 1/60², the tidal force on the nearest point is 1/59²−1/60², the tidal force on the furthest point is 1/60²−1/61², both of which are roughly 1/30 of the gravitational force.

The difference between the tidal force on the nearest and furthest point is thus (1/59²−1/60²)−(1/60²−1/61²) which is roughly 1/20 of the tidal force. This should show up on earth tides, if they could be measured accurately enough.

You can calculate tidal forces using the centrifugal force, as recommended by others, but it is much easier to use differential gravity as I have done.