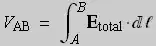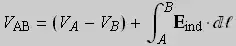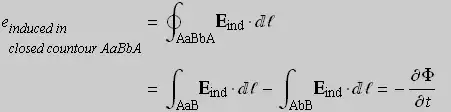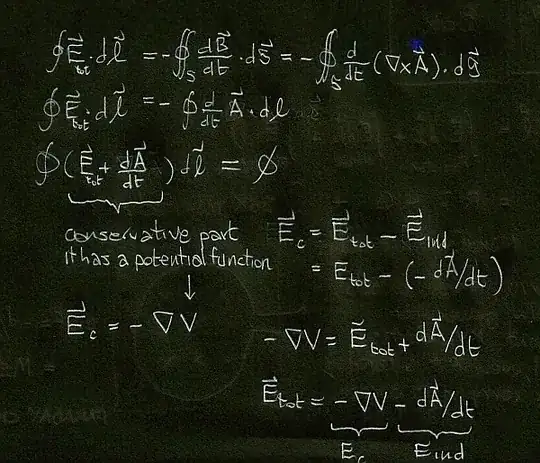Assigning a notion of voltage even when there is a changing magnetic field

Question

In Walter Lewin's lecture, he finds depending on how you keep the lead of the voltmeter for a circuit in a changing magnetic field, you will measure different values]. This experiment is discussed from 49:34 of this lecture and then infers that this is why a notion of voltage is no longer possible in the case of changing magnetic field.

According to Mr.Boom, Lewin's result had a correct result, given his setup, but his conclusion was incorrect. To demonstrate this Mr.Boom experiments (see from 7:24 of this video before disagreeing), where he creates a modified version where Lewin's concluded principle must be equally applicable, however in Mr. Boom's equivalent experiment, Lewin's ideal fails. Hence, the premise of Boom was demonstrated. Particularly speaking, Mr.Boom says that, and I quote from after 10:45 of the second video, he concludes the real reason for Lewin's result was bad probing (*)

however, Mehdi(Mr.Boom) does an experiment in his second video and gets a result against Lewin's theory, so what was wrong with the experiment for falsifying Lewin? I have read this answer by Sredni Vashtar on this but I am not able to use their answer to answer this doubt I have put in the sentence right before.

I think that there is a definite voltage for a circuit even with a field passing through because even though the voltage depends on the line integral, there is only one physical path where current can go through feasible in a circuit!.

---

Understanding Mr.Boom's arguments

The original experiment of Lewin involved the following circuit:

Now, using an oscilloscope ( I think?) he measures top and bottom point of circuit at same time (For Boom's discussion)

And finds that each scope shows different readings:

Mr. Boom repeats the experiments and finds the same results here, but he disagrees with the conclusion which Lewin made that this leads to KVL not be applicable in the case of circuits with varying magnetic field effects.

To illustrate his point, he does an experiment with a similar set up:

Since Lewin's theory must be independent of how resistors are arranged, Mr.Boom rearranges the resistors (1k and 10k )and then measures the voltage of each side. He begins by measuring on the 10k side:

This results into:

And then he measures through opposite side:

Which results in the reading:

He then measures the reading across both the resistor:

This resulting graph is the some of voltage graph of each resistor measured in individual case. Now, he says the sum voltage is the same voltage across the loop. Hence, there is indeed only a single voltage associated with the two points across the circuit. Now, to double check, he discusses the measurement if the sense wires the other way (path without resistor)

In this way, it seems that the voltage of the sense wire is zero.. and again we with multiple voltage values. Now, boom's explanation is that the problem is that the voltage is not single-valued but rather an accurate reading can not be taken as the induced field effects the measuring device as well. (see from 8:55 )

Note: All of the above is my understanding of boom's video, if there is a mistake please point out.

---

Physicists and Electronic engineers divided?

To be frank, I couldn't easily understand Mr. Boom's video, so I searched for other videos by people in electronic engineering-related fields for perhaps a more 'dumbed down' version of it to understand. This led me to this video by Mr. Bob Duhamel, in which he states that Lewin is wrong see from around 23:00 and agrees with Mr. Booms's result.

Now, here is the weird part, people in physics stack exchange and such seem to agree with Mr. Lewin's result that different measurements give different values see this answer by knzhou. So, it seems the answer is entirely different depending on wether you study EE or physics.

---

Romer's paper

So, now I saw the paper which roomer wrote on the issue (Mr.Boom cites this in 2nd video response). The paper is quite interesting and introduces a concept of 'pseudo potential' which can be assigned even in case of changing magnetic field and he explains this new idea with concepts of topology and such. He specifically finds that though the line integral of E*dl is indeed path-dependent, there are only two or three discrete values it can take.

I haven't fully understood the paper's significance here, I'll add in this part as I read through it more.

---

Some related questions on this aren't easily findable, so I will link all here:

1. Does Kirchhoff hold even when there is changing magnetic field?
2. Can two voltmeters connected to the same terminals show different values? Circuit with induced EMF ( See Sredni vashtar's answer)
3. What would a voltmeter measure if you had an electromotive force generated by a changing magnetic field?
4. Are Kirchhoff's Laws violated in case of varying magnetic fields?
5. Kirchhoff's Voltage Law in a General Electromagnetic Field

Hopefully, I got all the related posts, please comment if I have missed any because I want to bring a 'clear' to make myself completely clear what was going on here.

P.s: I have no formal education in Electronics engineering, only some basics I learned from high school. So please comment if I have made mistakes in understanding the situation in my post, I will correct them.

Further, apologies if this post seems a bit messy, I tried my best to make sense of everything I read from multiple resources and put in a neat summary here but I hope it makes sense.

Answer 1

Let me first answer to the question about how to define voltage in a changing magnetic field by using this extensive quote from Popovic & Popovic, "Introductory Electromagnetics", sec. 14.4 "Potential difference and voltage in a time-varying electric and magnetic field":

"In the discussion of electrostatics, we defined the voltage to be the same as the potential difference. Actually, the voltage between two points is defined as the line integral of the total electric field strength from one point to the other. In electrostatics, the induced electric field does not exist, and therefore voltage is identical to potential difference. [...] this is not the case in a time-varying electric and magnetic field. Consider arbitrary time-varying currents and charges producing a time-varying electric and magnetic field [...]. 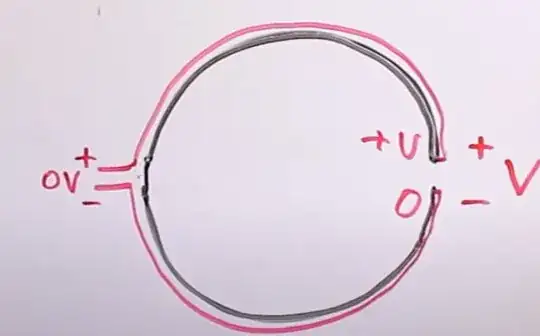Consider two points, A and B, in this field, and two paths, a and b, between them, as indicated in the figure. The voltage between these two points is defined as

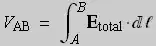
In this definition, Etotal is the total electric field strength, which means the sum of the "static" part (produced by charges) and the induced part (due to time-varying currents). We know that the integral between A and B of the static part is simply the potential difference between A and B. So we can write

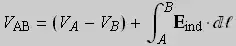
We know that the potential difference, VA - VB, does not depend on the path between A and B, but we shall now prove that the integral in this equation is different for paths a and b. These paths form a closed contour. Applying Faraday's law to that contour, we have

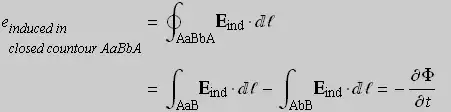
where \$\Phi\$ is the magnetic flux through the surface bounded by the contour AaBbA. Since the right side of this equation is generally nonzero, the line integrals of Eind from A to B along a and along b are different. Consequently, the voltage between two points in a time-varying electric and magnetic field depends on the particular path between these two points. This is an important practical conclusion. We always measure the voltage by a voltmeter with leads connected to the two points between which the voltage is being measured. Circuit theory postulates that this voltage does not depend on the shape of the voltmeter leads. We now know that in the time-varying case this is not true."

If you read my other answers on this topic, keep in mind that Popovic uses a different notation from the one I chose to use (it's just a sign difference in the definition, compensated by the reverse order of the starting and ending points), but there are no discrepancies.
Now let's get to the drama.

No build-up of voltage in the wires
The error that Mehdi commits, and many many others like him, is to assume that there is a voltage in the wires. (And by that I mean an appreciable voltage of about the portion of emf associated with the path, and not the tiny ohmic drop in copper.)
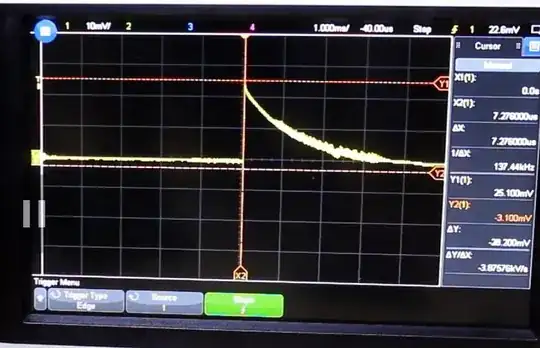
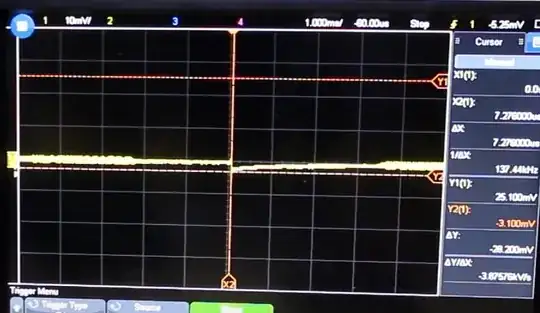
Here, from minute 11:20 of his first video

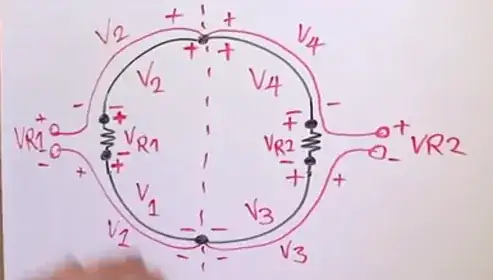
Let's focus on \$ V_1\$. There is no voltage, in the sense of path integral of the total electric field, there. There is a 'partial' voltage \$ V_1\$ that can be computed as the path integral of the induced \$E_{ind}\$ field there (and apart from the sign is equal to the path integral of the Coloumbian electric field there), but that field is only PART of the total field that happens to be there when the ring is placed in the field. The presence of the ring, and in particular of the copper conductor along the black arc indicated by V1, alters the total field because the free charge in the copper will redistribute themselves in order to establish a total field compatible with Ohm's law. Ideally, in a perfect conductor, the total field is zero in the wires. And it is zero thanks to the Coloumbian field generated by the charge that accumulates at the surface of the wire and at the interfaces with the resistive material.

The effect of this superposition makes the total electric field zero in the perfect conductor and different from zero only inside (and around) the resistors. The field inside the resistors will be compatible with Ohm's law there, namely \$E = j / \sigma_{res}\$, where \$\sigma_{res}\$ is the conductivity of the resistive material. With a real copper conductor, the field will not be exactly zero inside it, but it will assume a very small value compatible with Ohm's law there, namely \$E = j / \sigma_{copper}\$. With the currents in Lewin's ring it will be a handful of microvolts per meter.

This picture from my previous answer on the same topic shows the field inside the ring (supposedly shaped like a cylindrical torus of constant section and with clear cut interfaces between copper and resistive materials (imagine the arrows to be located inside the material the ring is made of)

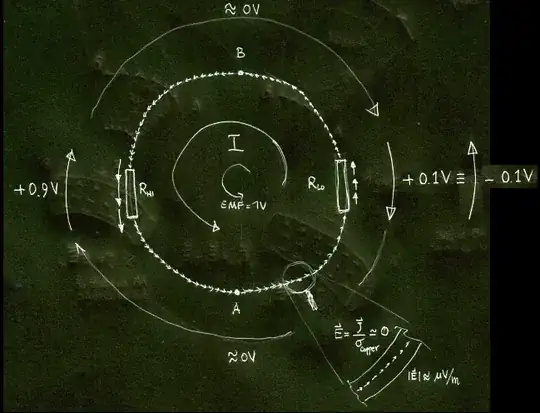
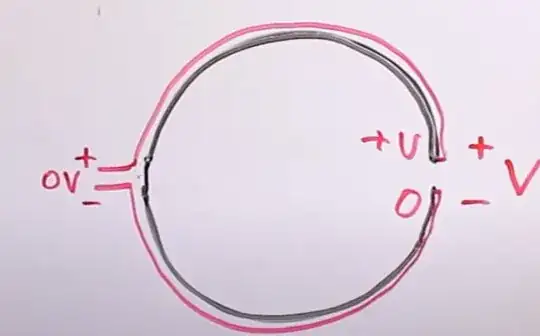
Multivalued voltage in the circuit itself: no probes required
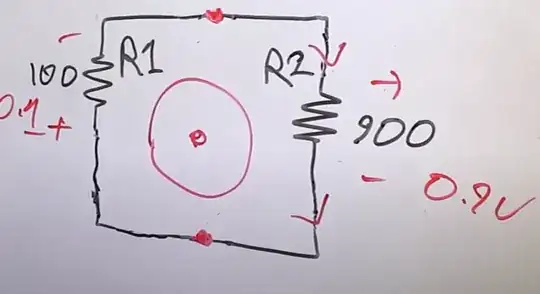
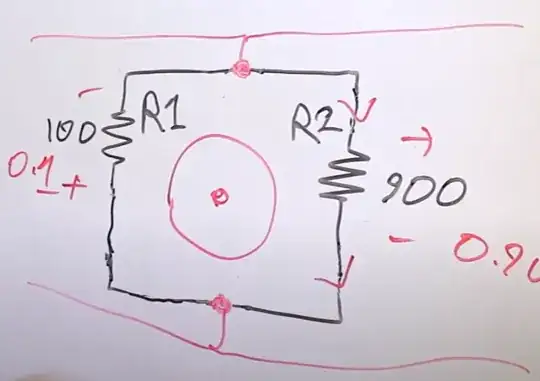
As you can see, if you compute the path integral of that total electric field from point A to point B you will obtain two different results depending on the path you choose: the path that goes through the bigger resistor will give +0.9V, while the path that goes through the smaller resistor will give you -0.1V. Yes, since the field is non-conservative, the path integral depends on the path, and not only on the endpoints. Also note that the sign is different, as well because the total electric field is 'rotational' (i.e. non-conservative).

But most importantly note that THERE ARE NO PROBES INVOLVED IN ALL THIS. This multivaluedness of the voltage is a property of the circuit and is a direct consequence of the fact that, by running the circuit path (and not a limited part of the system, hidden inside a magnetic component) around a variable magnetic field region, the electric field in the region of space occupied by the circuit path is not conservative.
That's all there is to it. Really.
Probes are not required to show this, and this is why the multivaluedness of voltage IS NOT a probing error. It's the way things are. Different from the oversimplified word of circuit analysis, but nonetheless that's how nature works. Lewin's probing is correct and shows how nature works.
Mehdi's, Mabilde's, VanMerveinne's and Duhamel's probing is not, because it shows a voltage corresponding to a partial electric field (namely the coloumbian conservative field they are accustomed to use in circuit theory). By running the probes at right angles with the induced electric field, they stripped the contribute of the induced field in the circuit and are left with the partial contribute of the coloumbian field only.
_{If you look at the parallel between the electrostatic and magneto-quasistatic phenomena in my other answer, it's as if instead of saying "the electrostatic field inside a conductor in an external field is zero", one would say "there is as electrostatic field inside the conductor because there are induced charges on its surface".}

Here's how to see the electric field decomposition in its conservative and solenoidal parts:

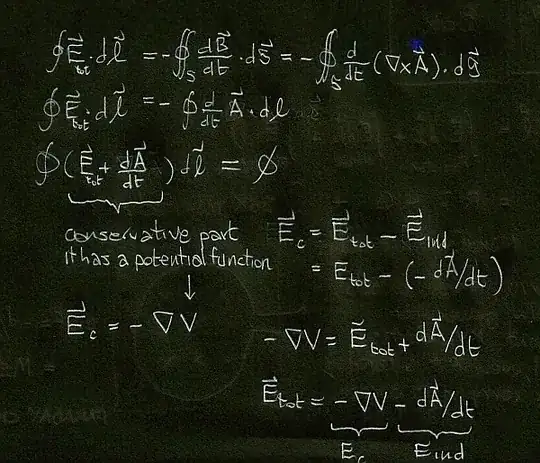
_{Note how the Coloumbian field Ec is only a part of the total electric field. In a perfect conductor Etot is zero (because zero resistivity implies infinite conductivity sigma and, by Ohm's law, E = j / sigma = 0 for finite current densities). This means that in the perfectly conducting wires connecting the resistors, we have Ec = -Eind.}

The above decomposition of fields mirrors the decomposition of voltage shown at the beginning of this answer.

Lumpable and unlumpable are not the same thing
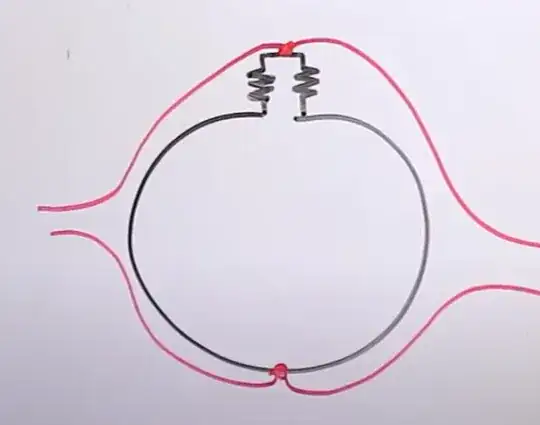
Engineers who incorrectly lump the Romer Lewin ring tend to think that there is a voltage build-up inside coils. There is none (Ramo Whinnery and VanDuzer show this clearly on p. 171 of the 2nd edition of "Fields and Waves in Communication Electronics"). The voltage appears at the terminals and in order to treat it as a potential difference (so that KVL can be used) it is necessary that the variable magnetic field that give rise to it be confined in a region of space that is OUTSIDE OF THE CIRCUIT PATH. Something that is not possible with the Romer-Lewin ring. Which is UNLUMPABLE.

Look at this picture:

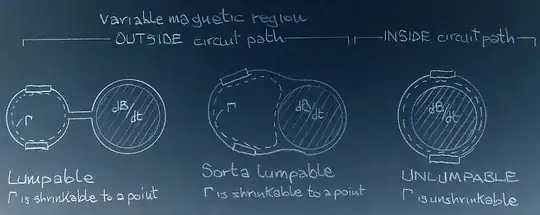
_{Lewin's circuit requires the two resistors to be on the opposite sides of the 'variable magnetic field region. You cannot stretch the circuit path by making the part with the resistors shrink to a point (imagine the resistors are points as well) as required by lumped circuit theory without forfeiting this geometric constraint.}

In lumpable circuits, KVL holds
The voltages in any point of the dashed circuit path Gamma of the first two circuits are uniquely defined and depends on endpoints alone; the voltages in the portion of system that is outside the dashed circuit path and run around the 'forbidden region', on the other hand, are path dependent. But they can still be hidden inside a component. The region around the dB/dt zone cannot be shrunk because the electrical properties depends on geometry and size; the region we associate with the circuit path gamma, on the other hand, can be shrunk to a point in what is the lumped circuit approximation. You can apply KVL (in its amended form that allows for lumped magnetic components) in a circuit that can be represented with the secondary of a transformer. This is what Mehdi did, believing he was still talking about Lewin's ring:

and he says "this shows that the voltage across the loop is not zero unlike what we've thought but it is equal to VR1 plus VR2. The loop is the secondary of a transformer, with the primary being my coil, KVL holds!". Thus demonstrating he does not understand the true nature of Lewin's ring and - by believing there is a voltage in the wires - not even how a (mutual) inductor works. He should read chapter 5 of Ramo Whinnery VanDuzer, or maybe Haus & Melcher.

In unlumpable circuits, KVL dies (but Faraday's thrive)
In the last circuit of the previous picture, i.e. Lewin's ring, the circuit path itself (and not a part of the system that is outside of it) goes around a variable magnetic field region in such a way that it is not possible to shrink it. Voltages IN THE CIRCUIT will be multivalued since they depends on path. See my answer to What would a voltmeter measure if you had an electromotive force generated by a changing magnetic field? to see the significance of being unable to move the variable field region outside of the circuit path.

And no, in this case, when you are constrained to have the circuit path going around the variable magnetic field region you cannot simlply extend your network with current sources, representing what that magnetic field does to the conductors.
If you try to lump the effects of the variable magnetic field in one, two or as many 'secondary coils' as you like, you are considering a different circuit, i.e. one where the circuit path \$\Gamma \$does NOT go around the magnetic field region. And you can see that from the fact that you will lose the nonuniqueness of voltage. It's a new circuit that is good for bean counting, though.

Right or wrong, you get the same numbers
So, why do Mehdi and so many engineers in here keep insisting to represent the effects of variable magnetic field into partial lumped elements?
They are so used to KVL that they cannot let go of it and try to apply it even when it is no longer legit to do so. There is a reason behind it, tho: by incorrectly lumping the effects of the magnetic field into the wires, one can still get the results right.
Incorrect lumping is a way to 'count the beans' that can show which parts of the circuit intercept the most induced field.
(As an aside: the concept of partial inductance - which relies heavily on the use of the vector potential A - is useful in the field of electromagnetic compatibility. But it has to be understood that the -dA/dt part of the total electric field is just... a part of it, not all of it).

A word of advice: when confronting people who believes KVL is always right and/or Lewin committed a probing error, you should ask them to which "current" of thought they belong. Because there are different incompatible views among them: some believe the ring is a transmission line, others that Lewin forgot about self-inductance, others think there is a voltage build up in the wires, and others still just rename Faraday's law "KVL". Notice, though, that those who say Lewin is correct and voltage is simply multivalued are all on the same page.

Answer 2

In Walter Lewin's lecture, he finds depending on how you keep the lead of the voltmeter, you will measure different values. Supposedly he discusses it in this video according to Mr.Boom, and then infers that this is why a notion of voltage is no longer possible in the case of changing magnetic field.

That's nonsense. Of course there's a notion of voltage in presence of a changing magnetic field. In fact, Maxwell's equation, which describe all electricity (unless you start looking at quantum levels), specifically describe that relationship!

So, cutting this discussion quite short:

Kirchhoff's equation holds for the circuit notation you know, as it's a direct result of the very math that holds together the basics of reality (Ampère's circuital law says: you take any closed loop and calculate the current density along that. Then you get a value proportional to the integral of the magnetic field that goes through the surface enclosed by that line.

Now, that circuit notation you know, with nodes, and lines representing conductors, assumes these conductors are infinitely short, have zero resistance and no current is induced in them (otherwise, you wouldn't just draw a line, but a resistor and/or a current source, right). If no current is induced, then *there can't be a net magnetic field permeating the loop formed by any conductors in a classical circuit.

I.e. the pure application of Kirchhoff's law states your magnetic fields are zero. If they aren't, you need to extend your network with current sources, representing what that magnetic field does to the conductors (again, in these linear network circuits, the conductors, and all elements, are assumed to be zero in size, so that a magnetic field can't have any effect, speed of light doesn't matter etc pp).

So, yes, Kirchhoff's law and changing magnetic fields, thereby induced currents, and hence voltages across any resistive elements, are compatible – if you know the limits of where to apply Kirchhoff's law. The circuit schematics that you're used to are, as a model of a circuit, not sufficient to define things like length, position of conductors to a magnetic field, so obviously, they themselves aren't appropriate to demonstrate this.

Answer 3

I think that there is a definite voltage for a circuit even with a field passing through because even though the voltage depends on the line integral, there is only one physical path where current can go through feasible in a circuit!.

I believe one needs to distinguish between the voltage drop from a point A to a point B along a give curve, (which I will call V) and (the negative of) the potential field (which I will call U) which exists when the E field is irrotational, i.e. \$\nabla \times E = 0\$.

Let us define a voltage drop as the amount of work performed against an E field required to move a charge along a curve from a given point on the curve to a second given point on the curve. That is,

$$ V = \int_{C_{a\rightarrow b}}E\cdot ds$$

Now, to understand the difference between a voltage drop (so defined) and a potential difference.

Faraday's Law states:

$$\nabla \times E = -\frac{1}{c}\frac{\partial B}{\partial t}$$

If there is no time-varying magnetic field, this implies that

$$\nabla \times E = 0$$

which means that E is a conservative field. Being a conservative field implies that E is the gradient of a potential function, (which is commonly called V, but we will call it U so as not to confuse it with V which we are using to represent a voltage drop.)

$$E = \nabla U$$

U, being a potential function implies that the voltage drop V from a to b is path independent. The voltage drop V from a to b is equal to the potential at b minus the potential at a. We call such a path independent voltage drop a potential difference.

Note that when a circuit is cut by a time-varying magnetic field, the E field is not conservative, and so there is no potential function. However, this does not entail that there is any ambiguity whatsoever in the voltage drop through a particular path segment.

Now, when you wrote:

I think that there is a definite voltage for a circuit even with a field passing through because even though the voltage depends on the line integral, there is only one physical path where current can go through feasible in a circuit!.

it isn't clear whether the "definite voltage for a circuit" is intended to refer to a path-independent potential difference, or a path-specified "voltage drop".

If one believes in a path independent potential difference in the presence of a time-varying magnetic field affecting one's circuit, then there is a very pointed question that must be answered.

• What is the potential difference between the test points in a Romer-Lewin type experiment?

Is it one of the measured values? If so, which one, and why choose that one? Is it neither of those measured values? If so, can you give a way to measure or calculate it?

Now, here is the weird part, people in physics stack exchange and such seem to agree with Mr. Lewin's result that different measurements give different values see this answer by knzhou. So, it seems the answer is entirely different depending on wether you study EE or physics.

I agree with Lewin that voltmeters attached "on different sides" of a Romer-Lewin type experiment will show different values. It is hard not to agree with such a conclusion as it is easily demonstrated, and has been demonstrated by Electroboom as well. That result is also predicted and explained by KVL.

I think the reason why EEs tend to have a problem with Prof. Lewin is related to his comments that "KVL" is for the birds, that using it is crime, etc.

Kirchhoff's voltage law states that the sum of all voltage drops in a closed loop is equal to the emf in that loop. Now, whenever there is no time varying magnetic field, the voltage drop between two points is path-invariant. This entails KVL. However, KVL is not simply a special case of Faraday's law when there is no time varying magnetic field. KVL applies to specific loops, and therefore specific paths. \$\frac{\partial B}{\partial t} = 0\$ entails that KVL will hold, but \$\frac{\partial B}{\partial t} \ne 0\$ does not entail that KVL will not hold.

For those who believe that KVL does not hold in a Romer-Lewin type experiment, I have the following question.

• How do you calculate what a particular volt-meter will read in a Romer-Lewin type experiment?

Do you not pick loops, and determine voltages or currents according to Ohms law, Faraday's Law AND KVL? Please provide an example of a calculation of what will be observed without recourse to KVL, or a law derivative of, or equivalent to, KVL.

so what was wrong with the experiment for falsifying Lewin?

My understanding of magnetically induced voltage, and I imagine the understanding of most physicists, is that a Faraday induced emf, i.e. an emf induced in a loop due to a changing magnetic field, applies only to a closed loop. [The loop does not have to be a closed "circuit", it may have an "infinite" resistance, but we cannot speak of the emf induced in "part" of a wire, unless that wire forms a loop.]

Consider the following diagram from Mehdi

Myself, and I imagine most physicists, would say that the reason the loop consisting of the black wire, the red wire, and the (not shown) volt-meter has zero voltage is because it does not enclose any flux. [Nearly enclosing flux does not count]. Mehdi's explanation is that the red wire and the black wire are affected by the same flux, and have equal and opposite emf's induced in them.

Mehdi's explanation is contrary to how I was taught to reason about magnetically induced emf. I won't go so far as to say he is wrong -- he gets the same answer as me, 0V net. But that line of reasoning is unacceptable to a wide group of people (which happens to include a lot of physicists).

It is only on the basis of this idea of emf induced in non-closed curves that Mehdi arrives at his own conclusion that Lewin's conclusions are based upon "bad probing". Since it is commonplace to reject the idea of emf induced in part of a loop, the charge of "bad probing" will not be convincing to many, and it is not convincing to me, even though Mehdi arrives at the same numerical result.

With the assumption that there is an induced emf in part of a loop, Mehdi arrives at the conclusion that there is a definite potential difference between any two points in the diagram above. However, his answer to "what is that voltage", is not satisfactory to me. He says it is the voltage found by connecting the test leads of the voltmeter directly across the line connecting A and B. While this specifies a way of obtaining a value which is unique, that particular choice seems arbitrary to me. Perhaps more importantly, I can't think of any useful purpose to assigning that particular value. That is, apart from telling us what a voltmeter will read in that condition, I can't think of any further calculations that can be done with that value. It wouldn't tell us anything about how any other part of the circuit will behave (as far as I know). If it allowed a useful prediction, I think Mehdi's choice of assigned potential difference would gain greater credibility.

Despite this flaw in Mehdi's explanation, I do agree with his conclusion that KVL is not broken, and disagree with Lewin's that KVL is broken. KVL, as least how I understand it, gives consistent and accurate results, even in the presense of changing magnetic fields. KVL as understood by others may or may not work.

Answer 4

Kirchoff's Voltage law will apply if you include the parasitic (mutual) inductance of any wires used in the physical construction of the circuit, calculate the complex impedance instead of just the real resistance, including any energy imparted from outside the simplified circuit (e.g. moving a magnet requires energy). Note that scope probe leads (and the associated "ground" leads) also add (mutual) inductance to any circuit.

If you leave parts of a circuit out of your calculations, the math will no longer apply to the circuit.