Note: $I_k$ is unit matrix and $O_k$ is the zero matrix of order $k$ in the following text.
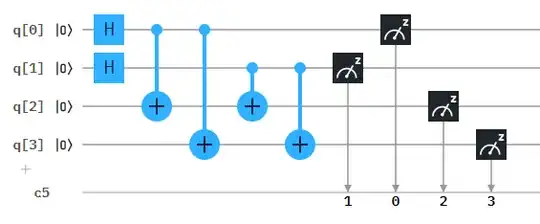
First step of the algorithm is $H \otimes H \otimes I_2 \otimes I_2$ as you mentioned.
A controlled gate $U$ with $n$ qubits between the control qubit and the target qubit can expressed as a matrix
$$
CU_{n} =
\begin{pmatrix}
I_{\frac{N}{2}} & O_{\frac{N}{2}} \\
O_{\frac{N}{2}} & I_{\frac{N}{4}} \otimes U
\end{pmatrix},
$$
where $N = 2^{n + 2}$ (you can check that for $n=0$ and $U=X$ you will get CNOT matrix).
Now, how to apply this on CNOT acting on $q_{2}$ and controlled with $q_{0}$. In this case $n=1$ and $U=X$. Hence $N=2^{1+2}=8$ and CNOT in the second step of algorithm can be written as
$$
CX_{1} =
\begin{pmatrix}
I_{4} & O_{4} \\
O_{4} & I_{2} \otimes X
\end{pmatrix}
$$
After that there is a $I$ gate on qubit $q_{3}$, so the second step of the algoritm can be written as $CX_{1} \otimes I_{2}$.
Third step is CNOT gate with two qubits between control and target qubits ($N=2^{2+2} = 16$) hence its matrix is
$$
CX_{2} =
\begin{pmatrix}
I_{8} & O_{8} \\
O_{8} & I_{4} \otimes X
\end{pmatrix}
$$
Fourth step is simply $I_2 \otimes CNOT \otimes I_2$.
Fifth step is $I_2 \otimes CX_{1}$ (i.e. similarly as in the second step but matrices in Kronecker product are switched).
You can check that all matrices describing each step is 16x16. Now, you can multiply them all together to get final matrix representation of the algorithm.