How can I construct the operator of a circuit with a controlled quantum gate where between the control and target qubits are other untouched qubits.
Given a controlled quantum gate $C(U) = I\oplus U$ where $U = \begin{bmatrix}u_0 & u_1 \\ u_2 & u_3\end{bmatrix}$.
The Operator for this circuit is simply $I\otimes C(U)$.
However, I'm not sure how to construct the operator for a circuit, where there are qubits in-between the control and target qubits. E.g.:
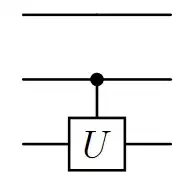
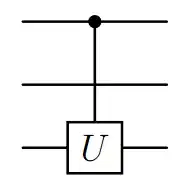
To construct a controlled gate with qubits in-between, you can use the following general form for a controlled gate:
$$U = |0\rangle\langle0| \otimes I + |1\rangle\langle1| \otimes G$$
Here, $|0\rangle\langle0|$ and $|1\rangle\langle1|$ are the projectors onto the states $|0\rangle$ and $|1\rangle$, respectively, and $I$ is the identity matrix. $G$ is the gate you want to apply when the control qubit is in state $|1\rangle$. Let's say you want to apply a controlled-NOT (CNOT) gate between qubits $q_1$ and $q_3$ with $q_2$ in-between. The controlled-NOT gate $G$ is represented as:
$$\text{CNOT} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}$$
The operator $U$ for this arrangement would be:
$$U = |0\rangle\langle0| \otimes I_2 + |1\rangle\langle1| \otimes \text{CNOT}$$
Here, $I_2$ is the 2x2 identity matrix. I hope this helps! Let me know if you need further clarification.
The controlled-unitary of your case is
$$|0\rangle\langle 0|\otimes \mathbb{1}\otimes \mathbb{1} + |1\rangle\langle 1| \otimes \mathbb{1}\otimes U.$$
In this example you can find the matrix (to the right of the circuit) for the controlled Hadamard. The elements with lower amplitudes correspond to the combinations with middle qubit being idle.
You can use this as guideline to build other unitaries, e.g. cnot.
