What exactly is an oracle
That's a great question, and even after studying 2 courses on quantum algorithms, this concept wasn't clear enough for me.
Mathematically, this is just as written above. For every classical function $f:\{0,1\}^n \rightarrow \{0,1\}$ a quantum oracle is defined as the unitary $U_f |x\rangle_n |y\rangle_1 = |x\rangle_n |y \oplus f(x)\rangle_1 $. So at the end 'it is just' the unitary that implements some function on a quantum computer.
However, some key questions that are usually swept under the rug:
- Why do we need these oracles?
- How to implement an oracle?
- A concrete example for an oracle?
So,
- Why do we need these oracles?
This is a mathematical concept (or a mathematical tool) that is useful when we design and analyze quantum algorithms. When analyzing algorithms it is common to analyze them in terms of how many times a specific building block is used. Often this building block is the oracle or black box function. Also when designing quantum algorithms, it is sometimes useful to have building blocks where we assume they implement some function, i.e. an oracle.
E.g. the following is an oracle written in Classiq's Qmod language (disclaimer - I’m a Classiq employee):
qfunc oracle_function(target: qbit, x: qnum) {
target ^= x == 0;
}
this oracle functions applies the oracle for the function $x==0$.
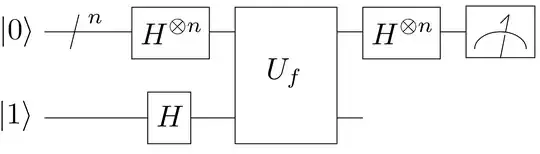
2.How to implement an oracle?
Using high-level functional design tools like Classiq it's quite easy. You design the function you want, and then the compiler synthesizes an underlying implementation. For the above example, this is the underlying circuit implementation for the oracle:
- A concrete example
A good example for the use of oracles in advanced algorithms is the discrete quantum walk. You can find a good resource for the theory of this in Andrew's Childs lecture notes chapter 17 and a concrete example in the Classiq git repo.
It's also worth noting the phase-kickback is a common primitive that is often used in the context of quantum oracles (see more here).
 ,
,